Just MTF Charts
Just the MTF Charts: 70-200mm f/4 Zoom Lenses

We did the 70-200mm f/2.8 lens MTF charts last week, so let’s do the f/4 versions of the same range now. Sports shooters and portrait photographers need that f/2.8 aperture, but many of us, most of the time, are willing to trade that off for smaller-lighter-less expensive f/4 models.
So, About f/4
Before we start, let me save someone from looking dumb on the internet. Not a week goes by that I don’t see someone use our MTF graphs to say something like “the f/4 is actually sharper than the f/2.8”, or “the f/2.8 is sharper than the f/1.4” yada, yada, yada. The complete sentence has to be “the f/4 is sharper at f/4 than the f/2.8 is at f/2.8”. Because stopped down means sharper, at least for the first stop or two.
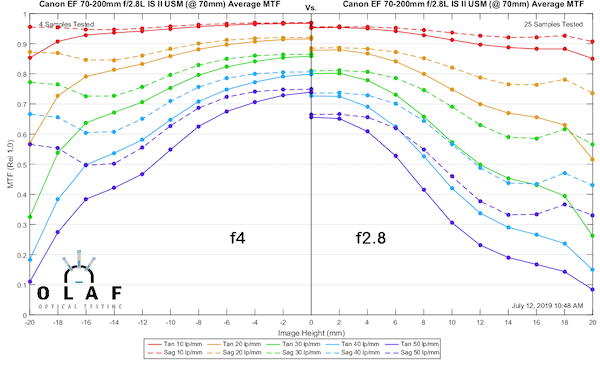
So let’s take a quick look at that f/2.8 to f/4 difference. I’ll use the Canon 70-200mm f/2.8 IS II as an example. Here are the MTF results at 70mm taken at f/2.8 and f/4.
Lensrentals.com, 2019
You can see there is a pretty dramatic improvement throughout almost all of the field of view by stopping down just one stop – at 70mm.
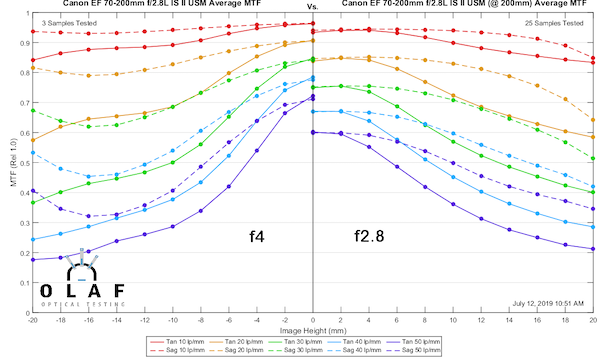
Let’s make the same comparison at 200mm. This time things are a little different. At f4 things are clearly sharper in the center of the image, but in the outer half, there’s no definite improvement. The curves are different, but not better.
Lensrentals.com, 2019
So why must I smite your quest for the Holy Grail of “just give me one number to evaluate the whole lens at all focal lengths and apertures and shooting conditions so I can go online and say the Wunderbar 70-200mm scores 74.2 which is better than Ubertoy 70-200mm which scores 73.7”? Because of optical physics, that’s why. Well, and also because it’s a stupid quest.
The reason things don’t always improve the same when you stop down is pretty straightforward. Remember, lenses have aberrations, which among other things reduce MTF. Some aberrations are dramatically improved or at least significantly improved by stopping down. Other aberrations are markedly worse the further you go from the center and not influenced very much by closing the aperture.
So, closing down one stop will make a massive difference in the center of the image; aperture-dependent aberrations (spherical aberration mostly, but also some types of coma) improve and the ‘distance-from-center’ dependent aberrations (astigmatism and some others) aren’t significant in the center.
Out at the edges of the image, stopping down makes some difference for many aberrations, but very little difference for others. Unless you know what aberrations the lens has, you can’t predict how much improvement stopping down makes, especially in the outer parts of the image.
I always love when someone rants online about ‘the edges are soft even stopped down so my lens must be defective.’ Lots of lenses don’t get really sharp at the edges no matter how much you stop down, others do, but none ever get as sharp on the edges as in the center.
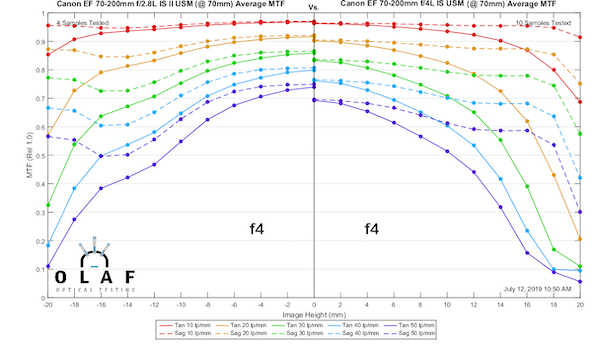
So let’s do a more practical test and compare the 70-200 f/2.8 IS at f/4 to the Canon 70-200mm f/4 IS II at 70mm and 200mm (the full f/4 curves are coming up later).
Lensrentals.com, 2019
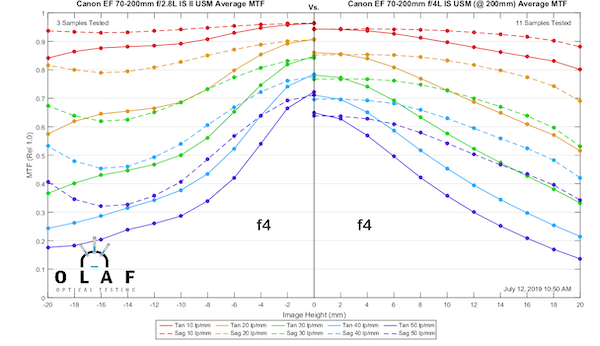
Lensrentals.com, 2019
The takeaway message, in this example, is that while the f/4 lens is arguably a tiny bit sharper than the f/2.8 at f/2.8, it is not sharper than the f/2.8 at f/4. It’s damn close, though.
The other takeaway message is you can’t be sure exactly how much and where (either image circle where or focal length where) a zoom lens will improve stopped down a stop. It will be better, but it’s difficult to predict precisely how much better without testing. And no, I don’t have the resources to do stop down testing on all the zooms. Even this little 3-copy example took a day’s testing and days are something I don’t have enough of.
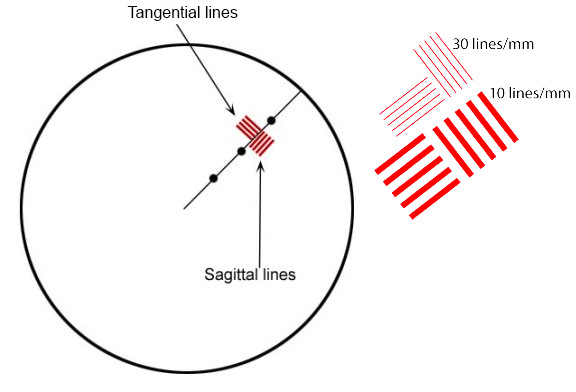
A Quick How to on Reading MTF ChartsIf you’re new here, you’ll see we have a scientific methodology to our approach, and use MTF charts to measure lens resolution and sharpness. All of our MTF charts test ten of the same lenses, and then we average out the results. MTF (or (or Modulation Transfer Function) Charts measure the optical potential of a lens by plotting the contrast and resolution of the lens from the center to the outer corners of the frame. An MTF chart has two axis, the y-axis (vertical) and the x-axis (horizontal). The y-axis (vertical) measures how accurately the lens reproduces the object (sharpness), where 1.0 would be the theoretical “perfect lens.” The x-axis (horizontal) measures the distance from the center of a lens to the edges (measured in millimeters where 0mm represents the center, and 20mm represents the corner point). Generally, a lens has the greatest theoretical sharpness in the center, with the sharpness being reduced in the corners. Tangential & Sagittal LinesThe graph then plots two sets of five different ranges. These sets are broken down into Tangential lines (solid lines on our graphs) and Sagittal (dotted lines on our graphs). Sagittal lines are a pattern where the lines are oriented parallel to a line through the center of the image. Tangential (or Meridonial) lines are tested where the lines are aligned perpendicular to a line through the center of the image. From there, the Sagittal and Tangential tests are done in 5 sets, started at 10 lines per millimeter (lp/mm), all the way up to 50 lines per millimeter (lp/mm). To put this in layman’s terms, the higher lp/mm measure how well the lens resolves fine detail. So, higher MTF is better than lower, and less separation of the sagittal and tangential lines are better than a lot of separation. Please keep in mind this is a simple introduction to MTF charts, for a more scientific explanation, feel free to read this article. |
Canon 70-200mm f/4L IS
This is the original Canon IS version that we introduced above. While I don’t have test results for the Non-IS it was considered a bit sharper than this original IS, but not as sharp as the IS II version below.
70mm
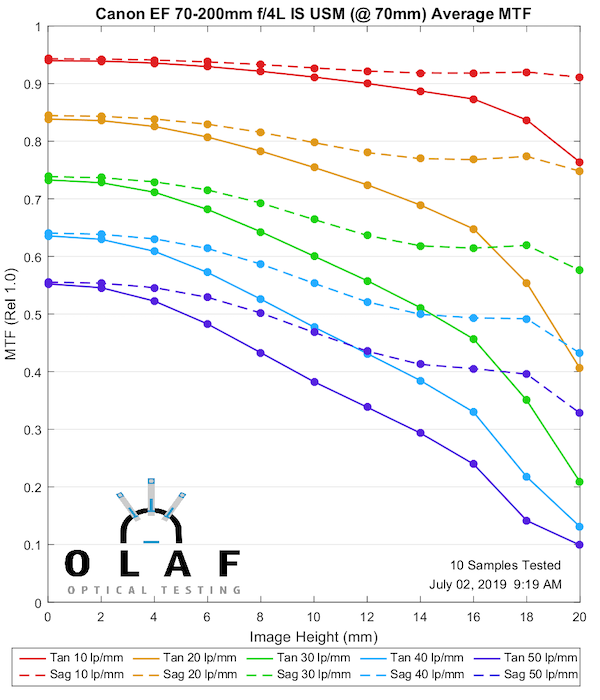
Lensrentals.com, 2019
135mm
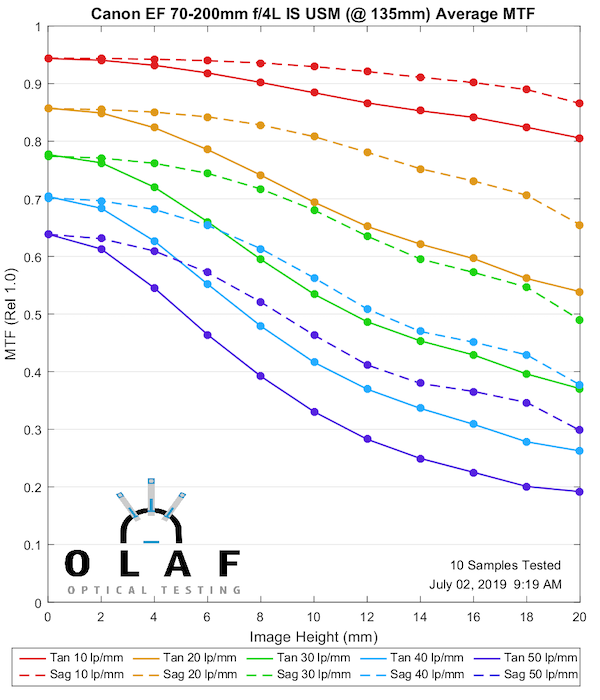
Lensrentals.com, 2019
200mm
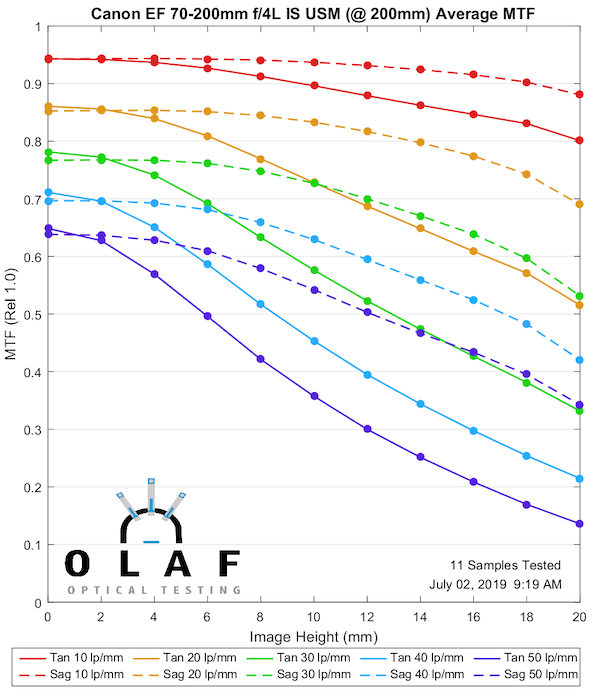
Lensrentals.com, 2019
Canon 70-200mm f/4L IS II
This makes a good second lens to show you because the version II is noticeably sharper than the original version at 70mm and 135mm. You can tell the difference if you shoot with them, so this gives you a good ‘this much difference is significant’ comparison for the other MTF charts. It is better at 200mm, but more at the ‘you’d have to make a careful direct comparison to see a difference’ level.
70mm
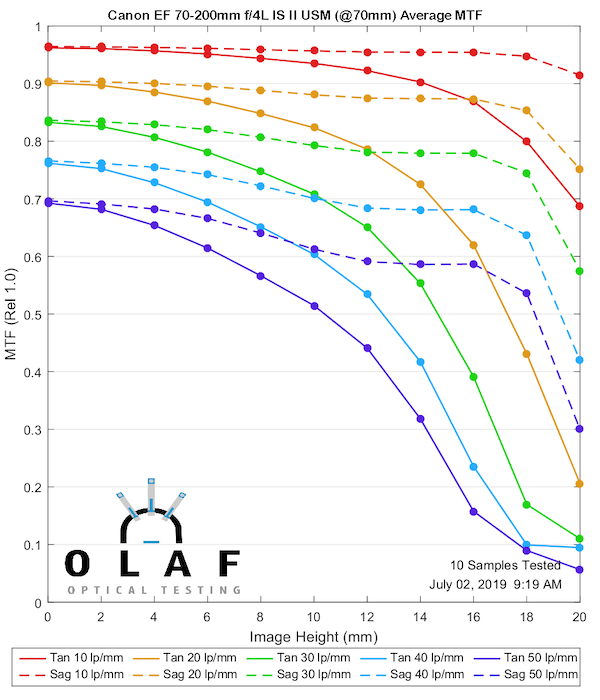
Lensrentals.com, 2019
135mm
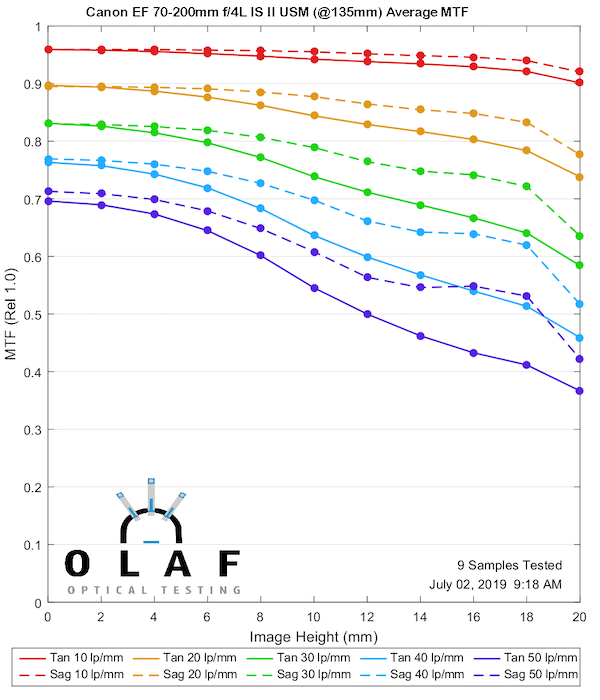
Lensrentals.com, 2019
200mm
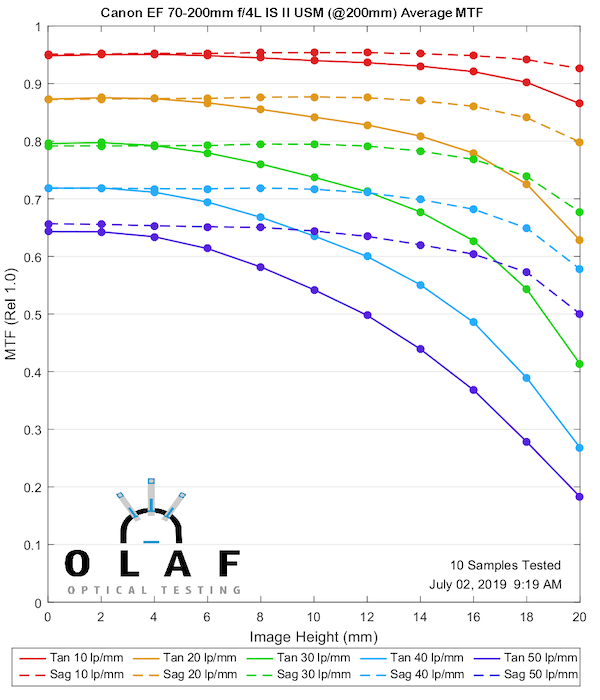
Lensrentals.com, 2019
Nikon AF-S 70-200mm f/4 G ED VR
Nikon makes the best f/2.8 zoom in this focal length, but their f/4 version is better described as ‘fine.’ It’s about as good as the original Canon version, maybe a bit better, but not as good as the Canon version II. The more paranoid among you can now begin discussions about ‘did they dumb-down the f/4 version so it couldn’t compete with the f/2.8?’ I can’t imagine that is true; designing lenses isn’t like turning off a video codec.
70mm
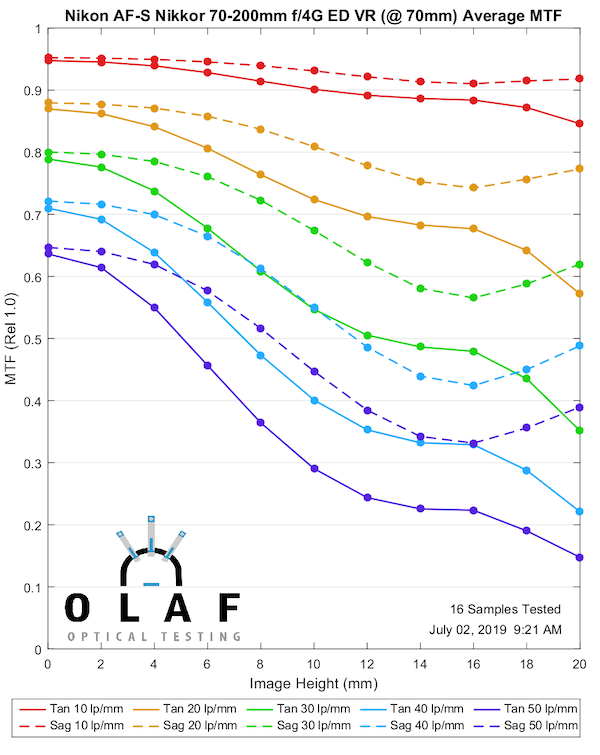
Lensrentals.com, 2019
135mm
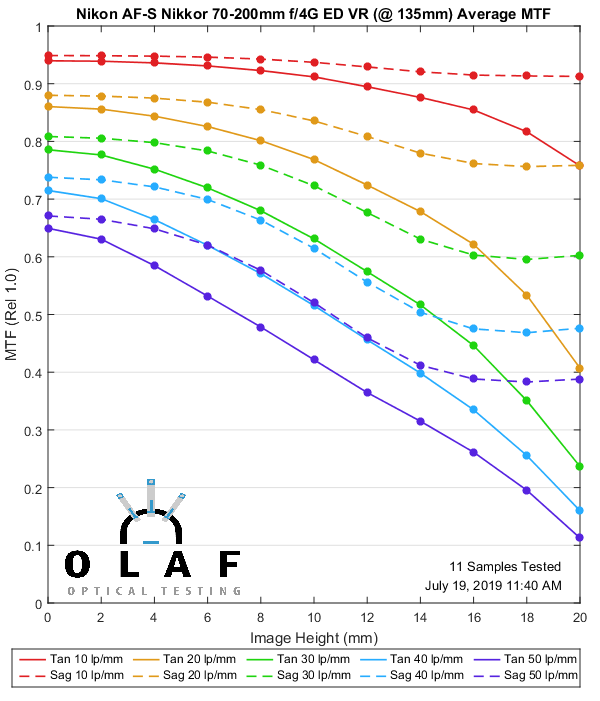
Lensrentals.com, 2019
200mm
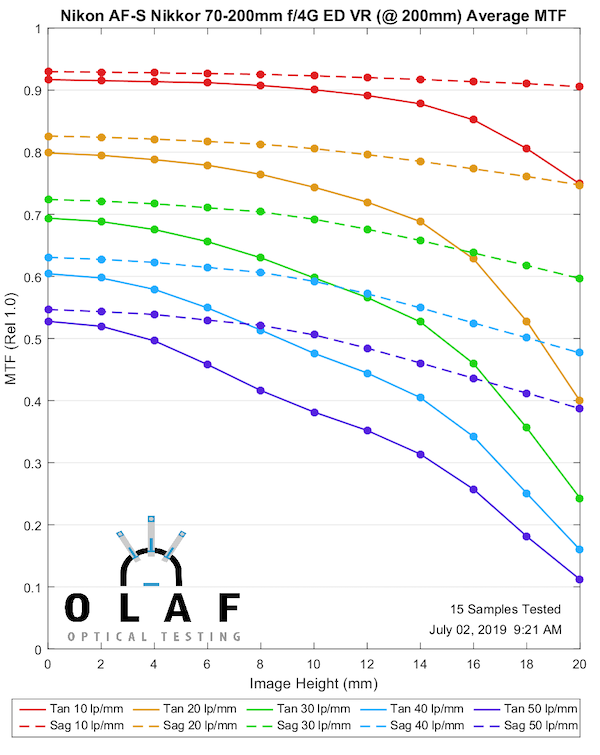
Lensrentals.com, 2019
Sony FE 70-200mm f/4 G OSS
Sony tends to put out more lenses per year than anyone else, and they have improved their lens quality rapidly over the last several years. But some of the older Sony designs are not great, and this is one of those. It’s at it’s best in the middle range, not quite as good at the two extremes. Some of you more strident Sony supporters will now state how wonderful it is and that the tests are wrong.
70mm
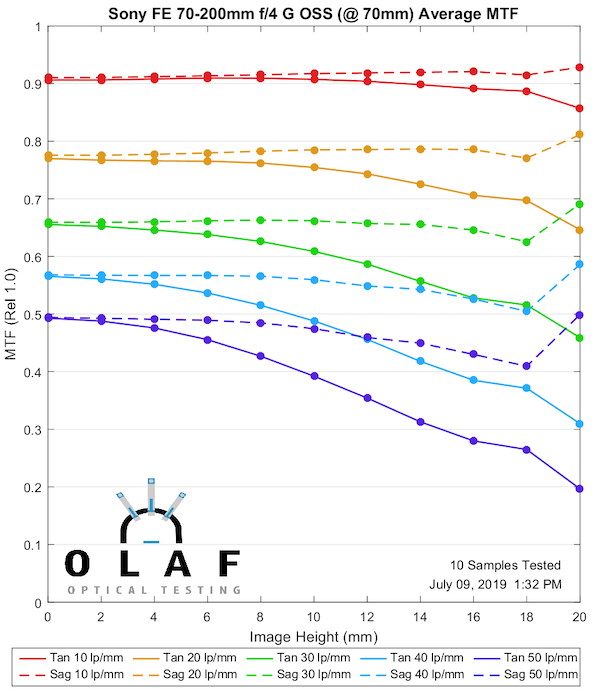
Lensrentals.com, 2019
135mm
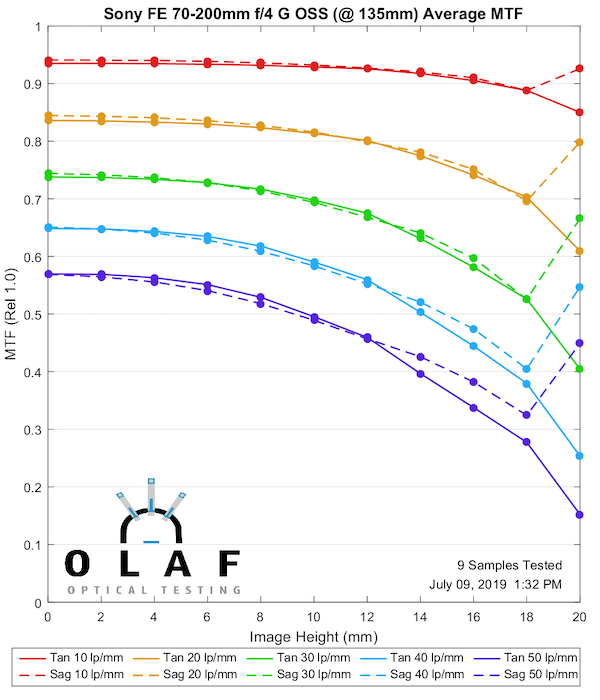
Lensrentals.com, 2019
200mm
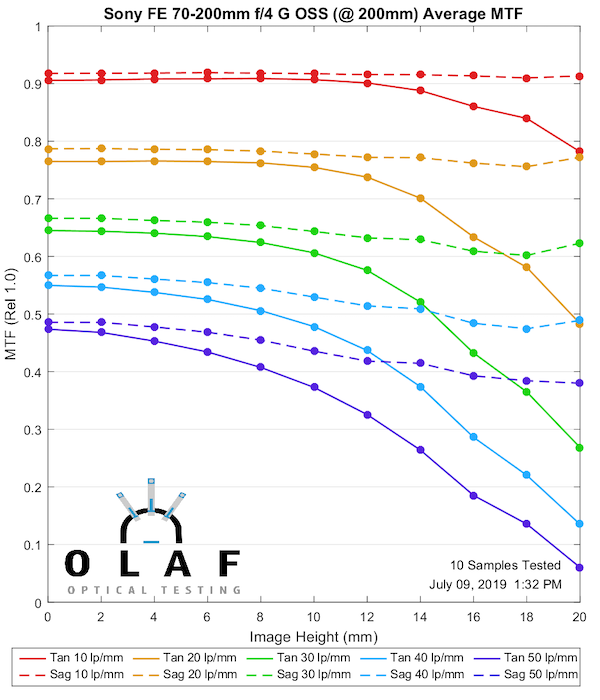
Lensrentals.com, 2019
Summary:
The conclusions here are pretty simple. If you shoot (or adapt) Canon EF mount lenses the Version II Canon 70-200mm f/4 IS II is excellent. It’s so good that you should only buy the 70-200mm f/2.8 version if you need f/2.8. (Since lots of people want the narrower f/2.8 depth of field for portraits or need all the light they can get for stop-motion action photography, the f/2.8 still will have lots of takers.)
The Nikon 70-200mm f/4 is good at 70mm and 135mm. While it fades a bit at 200mm it’s a really nice walk around and travel lens. The Nikon f/2.8 version is so good, though, that most people who can afford it will be willing to deal with the heavier lens and higher price for the image quality.
Sony also has a 70-200mm f/4, and it’s OK. It’s not going to wring all the resolution you might like out of a high-megapixel camera, but it’s still a decent travel lens. From what I hear, though, a lot of Sony shooters prefer the Canon IS II f/4 on an adapter, and I can understand that option, too.
Roger Cicala and Aaron Closz
Lensrentals.com
July, 2019
Author: Roger Cicala
I’m Roger and I am the founder of Lensrentals.com. Hailed as one of the optic nerds here, I enjoy shooting collimated light through 30X microscope objectives in my spare time. When I do take real pictures I like using something different: a Medium format, or Pentax K1, or a Sony RX1R.
-
Matti6950 .
-
Roger Cicala
-
Nicholas Bedworth
-
Brandon Dube
-
Chris
-
Ilya Snopchenko
-
Ashley Pomeroy
-
thepaulbrown
-
JordanCS13
-
Ciaran
-
Nicholas Bedworth
-
Max Manzan
-
Brandon Dube
-
Brandon Dube
-
Brandon Dube
-
Christopher J. May
-
Roger Cicala
-
Roger Cicala
-
Misha Engel
-
Christopher J. May
-
Roger Cicala
-
Roger Cicala
-
Misha Engel
-
asad137
-
geekyrocketguy
-
Franz Graphstill
-
Andreas Werle
-
Andreas Werle
-
asad137