Technical Discussions

Sensor Size Matters – Part 2

By
Published February 5, 2012

Why Sensor Size Matters

Part 1 of this series discussed what the different sensor sizes actually are and encouraged you to think in terms of the surface area of the sensors. It assured you the size of the sensor was important, but really didn’t explain how it was important (other than the crop-factor effect). This article will go into more detail about how sensor size, and its derivative, pixel size, affect our images. For the purists among you, yes, I know “sensel” is the proper term rather than “pixel.” This stuff is confusing enough without using a term 98% of photographers don’t use, so cut me some slack.

I’ve made this an overview for people who aren’t really into the physics and mathematics of quantum electrodynamics. It will cover simply “what happens” and some very basic “why it happens.”  I’ve avoided complex mathematics, and don’t mention every possible exception to the general rule (there are plenty). I’ve added an appendix at the end of the article that will go into more detail about “why it happens” for each topic and some references for those who want more depth.

I’ll warn you now that this post is too long – it should have been split into two articles. But I just couldn’t find a logical place to split it. My first literary agent gave me great advice for writing about complex subjects: “Tell them what you’re gonna tell them. Then tell them. And finally, tell them what you told them.” So for those of you who don’t want to tackle 4500 words, here’s what I’m going to tell you about sensor and pixel size:

  • Noise and high ISO performance: Smaller pixels are worse. Sensor size doesn’t matter.
  • Dynamic Range: Very small pixels (point and shoot size) suffer at higher ISO, sensor size doesn’t matter.
  • Depth of field: Is larger for smaller size sensors for an image framed the same way as on a larger sensor. Pixel size doesn’t matter.
  • Diffraction effects: Occur at wider apertures for both smaller sensors and for smaller pixels.
  • Smaller sensors do offer some advantages, though, and for many types of photography their downside isn’t very important.

If you have other things to do, are in a rush, and trust me to be reasonably accurate, then there’s no need to read further. But if you want to see why those 5 statements are true (most of the time) read on! (Plus, in old-time-gamer-programming style, I’ve left an Easter Egg at the end for those who get all the way to the 42nd level.)

Calculating Pixel Size

Unlike crop factor, which we covered in the first article, some of the effects seen with different sensor sizes are the result of smaller or larger pixels rather than absolute sensor size. Obviously if a smaller sensor has the same number of pixels as a large sensor, the pixel pitch (the distance between the center of two adjacent pixels) must be smaller. But the pixel pitch is less obvious when a smaller sensor has fewer pixels. Quick, which has bigger pixels: a 21 Mpix full-frame or a 12 Mpix 4/3 camera?

Pixel pitch is easy to calculate. We know the size of the camera’s sensor and the size of its image in pixels. Simply dividing the length of the sensor by the number of pixels along that length gives us the pixel pitch. For example, the full-frame Canon 5D Mk II has an image that is 5616 x 3744 pixels in size, and a sensor that is 36mm x 24mm.  36mm / 5616 pixels (or 23mm / 3744 pixels) =  0.0064mm/pixel (or 6.4 microns/pixel). We can usually use either length or width for our calculation since since the vast majority of sensors have square pixels.

To give some examples, I’ve calculated the pixel pitch for a number of popular cameras and put them in the table below.

Table 1: Pixel sizes for various cameras

 

 

 

Pixel size Camera
(microns)
8.4 Nikon D700, D3s
7.3 Nikon D4
6.9 Canon 1D-X
6.4 Canon 5D Mk II
5.9 Sony A900, Nikon D3x
5.7 Canon 1D Mk IV
5.5 Nikon D300s, Fuji X100
4.8 Nikon D7000, D800, Sony NEX 5n, Fuji X Pro 1
4.4 Panasonic AG AF100,
4.3 Canon GX1, 7D; Olympus E-P3
3.8 Panasonic GH-2, Sony NEX-7
3.4 Nikon J1 / V1
2.2 Fuji X10
2.0 Canon G12

A really small pixel size, like those found in cell phone cameras and tiny point and shoots, would be around 1.4 microns (1). To put that in perspective, if a full-frame camera had 1.4 micron pixels it would give an image of 25,700 x 17,142 pixels, which would be a 440 Megapixel sensor. Makes the D800 look puny, now, doesn’t it? Unless you’ve got some really impressive computing power you probably don’t have much use for a 440 megapixel image, though. Anyway, you don’t have any lenses that would resolve it.

Effects on Noise and ISO Performance

We all know what high ISO noise looks like in our photographs. Pixel size (not sensor size) has a huge effect (although not the only effect) on noise. The reason is pretty simple. Let’s assume every photon that strikes the sensor is converted to an electron for the camera to record. For a given image (same light, aperture, etc.) X number of photons hits each of our Canon G12’s pixels (these are 2 microns on each side, so the pixel is 4 square microns in surface area). If we expose our Canon 5D Mk II to the same image, each pixel (6.4 micron sides, so 41 square microns in surface area) will be struck by 10 times as many photons, sending 10 times the number of electrons to the image processor.

There are other electrons bouncing around in our camera that were not created by photons striking the image sensor (see appendix). These random electrons create background noise – the image processor doesn’t know if the electron came from the image on the sensor or from random noise.

Just for an example, let’s pretend in our original image one photon strikes every square micron of our sensor, and both cameras have a background noise equivalent to one electron per pixel. The smaller pixels of the G12 will receive 4 electrons from light rays reaching each pixel of the sensor (4 square microns) for each pixel of noise (4:1 signal-to-noise ratio) while the 5DII will receive 41 electrons from each pixel (41:1 signal-to-noise ratio). The electronic wizardry built into our camera may be able to make 4:1 and 41:1 look pretty similar.

But let’s then cut the amount of light in half, so only half as many photons strike each sensor. Now the SNR ratios are 2:1 and 20:1. Maybe both images will look OK. Of course we can amplify the signal (increase ISO) but that also increases the amount of noise in the camera. And if we cut the light in half again and the SNR is now 1:1 and 10:1. The 5DII still has a better SNR ratio at this lower light than the G12 had in the original image. But the G12 has no image at all: the signal (image) strength is no greater than the noise.

That’s an exaggerated example, the difference isn’t actually that dramatic. The sensor absorbs far more than 40 photons per pixel and there are several other factors that influence how well a given camera handles high ISO and noise. If you want more detail and facts, there’s plenty in the appendix and the references. But the takeaway message is smaller pixels have lower signal to noise ratios than larger pixels.

Newer cameras are better than older cameras, but . . . .

It is very obvious that newer cameras handle high ISO noise better than cameras from 3 years ago. And just as obvious is that some manufacturers do a better job handling high ISO than others (Some of them cheat a lot to do it, with in-camera noise reduction even in RAW images that can cause loss of detail – but that’s another article someday).

People often get carried away with this, thinking newer cameras have overcome the laws of physics and can shoot at any ISO you would please. They are better, there’s no question about it, but the improvements are incremental and steady. DxO optics has tested a lot of sensors for a pretty long time and has graphed the improvement they’ve seen in signal to noise ratio, normalized for pixel size. The improvement over the last few years is obvious, but on the order of 20% or so, not a doubling or tripling for pixels of the same size.

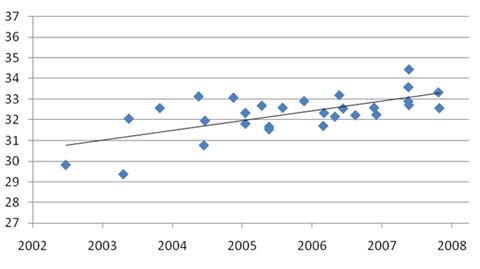
Signal to noise ratio, normalized for pixel size. (DxO optics)

 

Other things being equal (same manufacturer, similar time since release), a camera with bigger pixels has less noise than one with smaller pixels. DxO graphs ISO performance for all the cameras they test. If you look at the cameras with the best ISO performance (top of the graph) they aren’t the newest cameras, they’re the ones with the largest pixels. In fact, most of them were released several years ago.

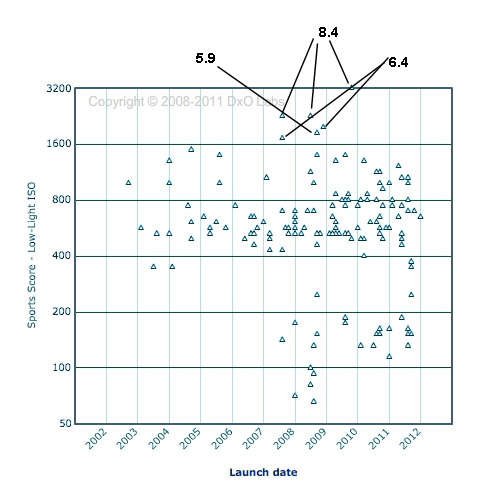
DxO Mark score for high ISO performance, with pixel size of the best cameras added.

The “miracle” increase in high ISO performance isn’t just about increased technology. It’s largely about decisions by designers at Canon, Nikon, and Sony in 2008 and 2009 to make cameras with large sensors containing large pixels. There is a simple mathematical formula for comparing the signal-to-noise ratio for different pixel sizes: the signal to noise ratio is proportional to the square root of the pixel pitch. There is more detail about it in the appendix.

Effects on Dynamic Range

You might think the effects of pixel size on dynamic range should be similar to that of noise, discussed above. However, dynamic range seems to be the area where manufacturers are making the greatest strides – at least with reasonably sized pixels. When measured at ideal ISO (ISO 200 for most cameras) dynamic range varies more by how recently the camera was produced than by how large the pixels are (at least until the pixels get quite small). If you look at DxO Mark’s data for sensor dynamic range the cameras with the best dynamic range are basically newer cameras, not those with the largest pixels.

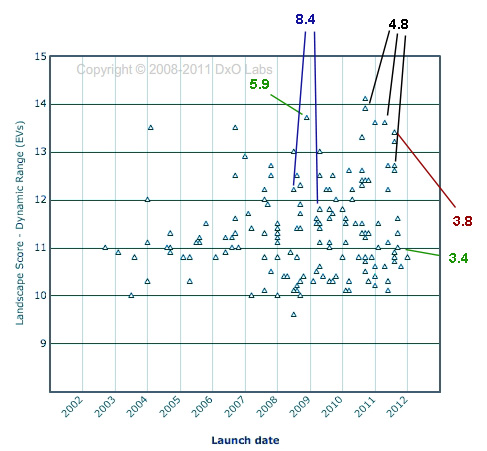
DxO Dynamic range scores with pixel sizes added for certain cameras. Recent release date seems much more important than pixel size.

 

There is no simple formula for calculating the effect of pixel size on dynamic range, but in general both large and medium size pixel sensors do well at low ISOs, but dynamic range falls more dramatically at higher ISOs for smaller pixels.

Effects on Depth of Field

Depth of field is a complex subject and takes some complex math to calculate. But the principles behind it are simple. To put it in words, rather than math, every lens is sharpest at the exact distance where it is focused. It gets a bit less sharp nearer and further from that plane. For some distance nearer and further from the plane of focus, however, our equipment and eyes can’t detect the difference in sharpness and for all practical purposes everything within that range appears to be at sharpest focus.

The depth of field is affected by 4 factors: the circle of confusion, lens focal length, lens aperture, and distance of the subject from the camera. Pixel size has no effect on depth of field, but sensor size has a direct effect on the circle of confusion, and the crop factor may also affect our choice of focal length and shooting distance. Depending on how you look at things, the sensor size can make the depth of field larger, shallower, or not change it at all. Let’s try to clarify things a bit.

Circle of Confusion

The circle of confusion causes a lot of confusion. But basically it is a measure of how large of a circle appears, to our vision, to be just a point (rather than a circle). It is determined (with a lot of argument about the specifics) from its size on a print. Obviously to make a print of a given size, you have to magnify a small sensor more than a large sensor. That means a smaller circle on the smaller sensor would be the limits of our vision, hence the circle of confusion is smaller for smaller sensor sizes.

There is more depth to the discussion in the appendix (and it’s actually rather interesting). But if you don’t want to read all that, below is a table of the circle of confusion (CoC = d/1500) size for various sensors.

 

Table 2: Circle of Confusion for Various Sensor Sizes

Sensor Size CoC
Full Frame 0.029 mm
APS-C 0.018 mm
1.5″ 0.016 mm
4/3 0.015 mm
Nikon CX 0.011 mm
1/1.7″ 0.006 mm

The bottom line is that the smaller the sensor size, the smaller the circle of confusion. The smaller the circle of confusion, the shallower the depth of field – IF we’re shooting the same focal length at the same distance. For example, let’s assume I take a picture with a 100mm lens at f/4 of an object 100 feet away. On a 4/3 sensor camera the depth of field would be 37.7 feet. On a full frame camera it would be 80.4 feet. The smaller sensor would have the shallower depth of field. Of course, the images would be entirely different – the one shot on the 4/3 camera would only have an angle of view half as large as the full frame.

That’s all well and good for the pure technical aspect, but usually we want to compare a picture of a given composition between cameras. In that case we have to consider changes in focal length or shooting distance and the effects those have on depth of field.

Lens Focal Length and Shooting Distance

In order to frame a shot the same way (have the same angle of view), with a smaller sensor camera we must either use a wider focal length, step back further from the subject, or a bit of both. If we use either a wider focal length, or shoot at a greater distance from the subject, keeping the same angle of view, then the depth of field will be increased. This increase  more than offsets the decreased depth of field you get from the smaller circle of confusion.

In the above example, I take a picture with a full-frame camera using a 100mm lens at a subject 100 feet distant at f/4. The depth of field was 80.4 feet. If I want to frame the picture the same way on a 4/3 camera I could use a 50mm lens (same distance and aperture). The depth of field would then be 313 feet. If instead I kept the 100mm lens but backed up to 200 feet distance to keep the same angle of view, the depth of field would be 168 feet. Either way, the depth of field for an image framed the same way will be much greater for the smaller sensor size than for the larger one.

So if we compare a similar image made with a small sensor or a large sensor, the smaller sensor will have the larger depth of field.

Compensating with a Larger Aperture

Since increasing the aperture narrows the depth of field, can’t we just open the aperture up to get the same depth of field with a smaller sensor as with a larger one? Well, to some degree, yes. In the example above the best depth of field I could get with a 4/3 sensor was 168 feet by keeping the 100mm lens and moving back to 200 feet. If I additionally opened the aperture to f/2.8 and then f/2.0 it would decrease the depth of field to 141 feet and 84 feet respectively. So in this case I’d need to open the aperture two stops to get a similar depth of field as I would using a full frame camera.

The relationships between shooting distance, focal length and aperture are complex and no one I know can keep it all in their head. If you move back and forth between formats a depth of field calculator is a must. And just to be clear: the effects on depth of field have nothing to do with pixel size, it’s simply about sensor size, whether the pixels on the sensor are large or small.

Effects on Diffraction

Everyone knows that when we stop a lens down too far the image begins to get soft from diffraction effects. Most of us understand roughly what diffraction is (light rays passing through an opening begin to spread out and interfere with each other). A few have gone past that and enjoy stimulating after-dinner discussions about Airy disc angular diameter calculations and determing Raleigh Criteria. A very few.

For the rest of us, here’s the simple version:  When light passes through an opening (even a big opening), the rays bend a bit at the edges of the opening (diffraction). This diffraction causes what was originally a point of light (like a star, for example) to impact on our sensor as a small disc or circle of light with fainter concentric rings around it. This is known as the Airy disc (first described by George Airy in the mid 1800s).

A computer generated Airy Disc (courtesy Wikepedia Commons)

The formula for calculating the diameter of the Airy disc is (don’t be afraid, I have a simple point here, I’m not going all mathematical on you):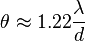 \theta \approx 1.22 \frac{\lambda}{d}

The point of the formula is to show you that the diameter of the airy disc is determined entirely by ? (the wavelength of light) and d (the diameter of the aperture). We can ignore the wavelength of light and just say in words that the Airy disc gets larger as the aperture gets smaller. At some point, obviously, the Airy disc gets large enough to cause diffraction softening.

At what point? Well, using the formula we can calculate the size of the Airy disc for every aperture (we have to choose one wavelength so we’ll use green light).

Table 3: Airy disc size for various apertures

Airy disc
Aperture (Microns)
f/1.2 1.6
f/1.4 1.9
f/1.8 2.4
f/2 2.7
f/2.8 3.7
f/4 5.3
f/5.6 7.5
f/8 10.7
f/11 14.7
f/13 17.3
f/16 21.3
f/22 29.3

Remember the circle of confusion we spoke of earlier? If the Airy disc is larger than the circle of confusion then we have reached the diffraction limit – the point at which making the aperture smaller is actually softening the image. In Table 2 I listed the size of the CoC for various sensor sizes. A smaller sensor means a smaller CoC so the diffraction limit occurs at a smaller aperture. Comparing the CoC (Table 2) with Airy disc size (Table 3) it’s apparent that a 4/3 sensor is becoming diffraction limited by f/11, a nikon J1 by  f/8, and a 1/1.7″ crop sensor camera between f/4 and f/5.6.

But the size of the sensor gives us the highest possible f-number we can use before diffraction softening sets in. If the pixels are small they may cause diffraction softening at an even larger aperture (smaller f-number). If the Airy disc diameter is greater than 2 (or 2.5 or 3 – it’s arguable) pixel widths then diffraction softening can occur. If we calculate when the Airy disc is larger than 2.5 x the pixel pitch rather than when it is larger than the sensor’s circle of confusion things look a bit different.

Table 4: Diffraction limit for various pixel pitches

 

 

 

Pixel Pitch 2.5 * PP Example camera Diffraction at
8.4 21 Nikon D700, D3s f/16
7.3 18.3 Nikon D4 f/13
6.9 17.3 Canon 1D-X f/13
6.4 16.0 Canon 5D Mk II f/12
5.9 14.8 Sony A900, Nikon D3x f/11
5.7 14.3 Canon 1D Mk IV f/11
5.5 13.8 Nikon D300s, Fuji X100 f/10
4.8 12.0 Nikon D7000, D800, Sony NEX 5n, Fuji X Pro 1 f/9
4.4 11.0 Panasonic AG AF100, f/8
4.3 10.8 Canon GX1, 7D; Olympus E-P3 f/8
3.8 9.5 Panasonic GH-2, Sony NEX-7 f/8
3.4 8.5 Nikon J1 / V1 f/6.3
2.2 5.5 Fuji X10 f/4.5
2 5.0 Canon G12 f/3.5

Let me emphasize that neither of the tables above are absolute values. There are a lot of variables that go into determining where diffraction softening starts. But whatever variables you choose, the relationship between diffraction values and sensor or pixel size remains: smaller sensors and smaller pixels suffer diffraction softening at lower apertures than do larger sensors with larger pixels.

Advantages of Smaller Sensors (yes, there are some)

There are several advantages that smaller sensors and even smaller pixels bring to the table. All of us realize the crop factor can be useful in telephoto work (and please don’t start a 30 post discussion on crop factor vs magnification vs cropping). The practical reality is many people can use a smaller or less expensive lens for sports or wildlife photography on a crop-sensor camera than they could on a full-frame.

One positive of smaller pixels is increased resolution. This seems self-evident, of course, since more resolution is generally a good thing. One thing that is often ignored, particularly when considering noise, is that noise from small pixels is often less objectionable and easier to remove than noise from larger pixels.  It may not be quite as good as it sounds in some cases, however, especially if the lens in front of the small pixels can’t resolve sufficient detail to let those pixels be effective.

An increased depth-of-field can also be a positive. While we often wax poetic about narrow depth of field and dreamy bokeh for portraiture, a huge depth of field with nearly everything in focus is a definite advantage with landscape and architectural work. And there are simple practical considerations: smaller sensors can use smaller and less expensive lenses, or use only the ‘sweet spot’ – the best performing center of larger lenses.

Like everything in photography: a different tool gives us different advantages and disadvantages. Good photographers use those differences to their benefit.

Summary:

The summary of this overlong article is pretty simple:

  • Very small pixels reduce dynamic range at higher ISO.
  • Smaller sensor size give an increased depth of field for images framed the same way (same angle of view).
  • Smaler sensor sizes have diffraction softening at wider apertures compared to larger sensors.
  • Smaller pixels have increased noise at higher ISOs and can cause diffraction softening at wider apertures compared to larger sensors.
  • Depending on what your style of photography these things may be disadvantages, advantages, or matter not at all.

Given the current state of technology, a lot of people way smarter than me have done calculations that indicate what pixel size is ideal – large enough to retain the best image quality but small enough to give high resolution. Surprisingly they usually come up with similar numbers: between 5.4 and 6.5 microns (Ferrel, Chen). When pixels are smaller than this the signal-to-noise ratio and dynamic range starts to drop, and the final resolution (what you can actually see in a print) is not as high as the number of pixels should theoretically deliver.

Does that mean you shouldn’t buy a camera with pixel sizes smaller than 5.4 microns? No, not at all. There’s a lot more that goes into the choice of a camera than that. And this seems to be the pixel size where disadvantages start to occur. It’s not like a switch is suddenly thrown and everything goes south immediately. But it is a number to be aware of. With smaller pixels than this you will see some compromises in performance – at least in large prints and for certain types of photography. It’s probably no coincidence that so many manufacturers have chosen the 4.8 micron pixel pitch as the smallest pixel size in their better cameras.

APPENDIX AND AMPLIFICATIONS

Effects on Noise and ISO Performance

A camera’s electronic noise comes from 3 major sources. Read noise is generated by the camera’s electronic circuitry and is fairly random (for a given camera – some cameras have better shielding than others). Fixed pattern noise comes from the amplification within the sensor circuitry (so the more we amplify the signal, which is what we’re doing when we increase ISO, the more noise is generated). Dark currents or thermal noise are electrons that are generated from the sensor (not from the rest of the camera or the amplifiers) without any photons impacting it. Dark current is temperature dependent to some degree so is more likely with long exposures or high ambient temperatures.

The example I used in this section is very simplistic and the electron and photon numbers are far smaller than reality. The actual SNR (or Photon/Noise ratio) is  P/(P + r2 + t2)1/2 where P = photons, r= read noise and t= thermal noise. The photon Full Well Capacity (how many photons completely saturate the pixel’s ability to convert them to electrons), read noise and dark noise can all be measured and the actual data for a sensor or pixel calculated at different ISOs. The Reference Articles by Clark listed below present this in an in-depth yet readable manner and also present some actual data samples for several cameras.

If you want to compare how much difference pixel size makes for camera noise, you can do so pretty simply: the signal to noise ratio is proportional to the square root of the pixel pitch. For example, it should be a pretty fair to compare the Nikon D700 (8.4 micron pixel pitch, SqRt = 2.9) with the D3X (5.9 micron PP, SqRt = 2.4) and say the D3X should have a signal to noise ratio that is 2.4/2.9 = 83% of the D700. The J1/V1 cameras with its 3.4 micron pixels (SqRt = 1.84) should have a signal-to-noise ratio that is 63% of the D700. If, in reality, the J1 performs better than that when actually measured, we can assume Nikon made some technical advances between the release of the D700 and the release of the J1.

Effects on Dynamic Range

At their best ISO (usually about ISO 200) most cameras, no matter how small the sensor size, have an excellent dynamic range of 12 stops or more. As ISO increases, larger pixel cameras retain much of their initial dynamic range, but smaller pixels loose dynamic range steadily. Some of the improvement in dynamic range in more recent cameras come from improved Analogue to Digital (A/D) converters using 14 bits rather than 12 bits, but there are certainly other improvements going on.

Effects on Depth of Field

The formulas for determining depth of field are complex and varied: different formulas are required for near distance (near the focal length of the lens) such as in macro work and for normal to far distances. Depth of field even varies by the wavelength of light in question. Even then, calculations are basically for light rays entering from near the optical axis. In certain circumstances off-axis (wide angle) rays may behave differently. And after the calculations are made, practical photography considerations like diffraction blurring must be taken into account.

For an excellent and thorough discussion I recommend the Paul van Walree’s (Toothwalker) article listed in the references. For the two people who want to know all the formulas involved, the wikepedia reference contains them all, as well as their derivation.

Circle of Confusion

Way back when, it was decided that if we looked at an 8 X 10 inch image viewed at 10 inches distance (this size and distance were chosen since 8 X 10 prints were common and 10 inches distance placed it at the normal human viewing angle of 60 degrees) a circle of 0.2mm or less appeared to be a point. Make the circle 0.25mm and most people perceive a circle; but 0.2mm, 0.15mm, 0.1mm, etc. all appear to be just a tiny point to our vision (until it gets so small that we can’t see it at all).

Even if a photograph is blurred slightly, as long as the blur is less than the circle of confusion, we can’t tell the difference just by looking at it. For example in the image below the middle circle is actually smaller and sharper than the two on either side of the middle, but your eyes and viewing screen resolution prevent you from noticing any difference. If the dots represent a photograph from near (left side) to far (right side) we would say the depth of field covers the 3 central dots: the blur is less than the circle of confusion and they look equally sharp. The dots on either side of the central 3 are blurred enough that we can notice it. They would be outside the depth of field.

To determine the Circle of Confusion on a camera’s sensor we have to magnify the sensor up to the size of an 8 X 10 image. A small sensor will have to be magnified more than a large sensor to reach that size, obviously.

There is a simple formula for determining the Circle of Confusion for any sensor size: CoC = d / 1500 where d = diameter of the sensor. (Some authorities use 1730 or another number in place of 1500 because they define the minimum point we can visualize differently, but the formula is otherwise unchanged.) But whatever is used, the smaller the diameter of the sensor, the smaller the circle of confusion.

Effects on Diffraction

Discussing diffraction means either gross simplification (like I did above) or pages of equations. Frighteningly (for me at least) Airy caclulations are the least of it. There also  is either Fraunhofer diffraction or Fresnel diffraction depending on the aperture and distance from the aperture in question, and a whole host of other equations with Germanic and old English names. If you’re into it, you already know all this stuff. If not, I’d start with Richard Feynman’s book QED: The Strange Theory of Light and Matter before tackling the references below.

If you want just a little more information, though, written in exceptionally understandable English with nice illustrations, I recommend Sean McHugh’s article from Camridge in Colour listed in the references. He not only covers it in far more detail than I do, he includes great illustrations and handy calculators in his articles.

One expansion on the text in the article. You may wonder why an Airy disc larger than 1 pixel doesn’t cause diffraction softening, why we choose 2, 2.5 or 3 pixels instead. It’s because the Bayer array and AA filter mean one pixel on the sensor is not the same as one pixel in the print (damn, that’s the first time ever I’ve thought that ‘sensel’ would be a better word than ‘pixel’). The effects of Bayer filters and AA filters are complex and vary from camera to camera, so there is endless argument about which number of pixels is correct. It’s over my head – every one of the arguments makes sense to me so I’m just repeating them.

Oh, Yeah, the Easter Egg

If you’ve made it this far, here’s something you might find interesting.

You’ve probably heard of the Lytro Light-Field Camera that supposedly lets you take a picture and then decide where to focus later. Lytro is being very careful not to release any meaningful specifications (probably because of skeptics like me who are already bashing the hype). But Devin Coldewey at TechCrunch.com has looked at the FCC photos of the insides of the camera and found the sensor is really quite small.

Sensor size of the Lytro Light Field Camera, courtesy TechCrunch.com

Lytros has published photos all over the place showing razor-sharp, narrow depth of field obtained with this tiny sensor.  Buuuuutttt, given this tiny sensor, as Shakespeare would say, “I do smelleth the odor of strong fertilizer issuing forth from yon marketing department.” Focus on one part of the image after the shot? Even with an f/2.0 lens in front of it, at that sensor size the whole image should be in focus. Perhaps blur everywhere else after the shot? Why, wait a minute . . . you could just do that in software, now couldn’t you?

REFERENCES:

R. N. Clark: The Signal-to-Noise of Digital Camera Images and Comparison to Film

R. N. Clark: Digital Camera Sensor Performance Summary

R. N. Clark: Procedure for Evaluating Digital Camera  Sensor Noise, Dynamic Range, and Full Well Capacities.

P. H. Davies: Circles of Confusion. Pixiq

R. Fischer and B. Tadic-Galeb: Optical System Design, 2000, McGraw-Hill

E. Hecht: Optics, 2002, Addison Wesley

S. McHugh: Lens Diffraction and Photography. Cambridge in Colour.

P. Padley: Diffraction from a Circular Aperture.

J. Farrell, F. Xiao, and S. Kavusi: Resolution and Light Sensitivity Tradeoff with Pixel Size.

P. van Walree: Depth of Field

Depth of Field – An Insider’s LookBehind The Scenes Zeiss Camera Lens News #1, 1997

http://en.wikipedia.org/wiki/Circle_of_confusion

Depth of Field Formulas: http://en.wikipedia.org/wiki/Depth_of_field#DOF_formulas

R. Osuna and E. García: Do Sensors Outresolve Lenses?

T. Chen, et al.: How Small Should Pixel Size Be? SPIE

 

Roger Cicala

Lensrentals.com

February, 2012

Author: Roger Cicala

I’m Roger and I am the founder of Lensrentals.com. Hailed as one of the optic nerds here, I enjoy shooting collimated light through 30X microscope objectives in my spare time. When I do take real pictures I like using something different: a Medium format, or Pentax K1, or a Sony RX1R.

Tweet
Posted in Technical Discussions
←  Older Comments
 →
  • Bob Newman

    Hi Roger,
    I’ve just been referred to this article form DPR. Ref your ‘If you want just a little more information, though, written in exceptionally understandable English with nice illustrations, I recommend Sean McHugh’s article from Camridge in Colour listed in the references. He not only covers it in far more detail than I do, he includes great illustrations and handy calculators in his articles.’ – that really is poor advice. That particular article is riven with technical bloopers and has misinformed a whole load of people about the relationship between pixel size and diffraction (a lot of that site is dodgy, by the way, refer with care). Your Table 4 refers to no kind of reality. Just look at your own excellent testing and see if you really can see ‘diffraction’ ‘kicking in’ at f/16 on a D3s and f/13 on a D4. There is no qualitative difference between the MTF graphs of a lens on a D3s and D4 at those f-numbers, there is just a steady rolloff, with the D4 giving hogher resolution at all f-numbers. Frankly, the theory as expounded by Sean McHugh and reported by you does not match observed reality. I see bobkcure below made a similar comment, 8 moths ago. Worth a revisit?

  • bobkoure

    Roger,
    Thanks for taking the time to write/post this!
    I notice you have a table of apertures and diffraction. From what I remember of physics (not much!), I would have thought that the relation was between diffraction and actual the physical size of the opening. F-stops are relative numbers, and even at a single focal length, it’s not clear to me that there’s a definite relationship between f-stops and diameter (don’t they play games with this in single-aperture zoom lenses?)
    Sorry to bring this up, but I’ve been puzzling over this since I first learned of diffraction as an issue.
    Thanks again!

  • Raul Rodriguez

    “Diffraction effects: Occur at wider apertures for both smaller sensors and for smaller pixels” I think that should be “narrower apertures” but I’m not te expert here.

  • Jon

    I calculated a 350D has a pixel size of 22.2mm/3456 pixels = 6.4microns which is the same as the 5d mark iii.

    You started: “Noise and high ISO performance: Smaller pixels are worse. Sensor size doesn’t matter”

    Why does the 5d3 have MUCH better noise performance than the 350D? Obviously it is not just the pixel pitch that is important here.

    🙂

  • john wewege

    I am into action photography (wild life and sports) and wish to purchase a fixed lens bridge camera:
    1) Which sensor size and pixel count would be better?
    2) Would a smaller zoom (e.g. x24) with a larger aperture (e.g. f2.8) throughout the zoom range be better than a larger zoom (e.g. x 50) with a smaller aperture that is not the same throughout the zoom range (e.g. f/3.4W; f/6.5T)?

  • Nqina Dlamini

    I’m reading this for the second time. Quite informative. I shall follow the Physics links and read more on the equations and the rest.
    Thank you.

  • I found this to be an compelling read. Mind going more into what sources you drew some of your statements from?

  • Carl

    Where did I claim it did? And since you think it hasn’t, perhaps you are admitting your initial generalization is also inaccurate. I do look forward to mankind’s knowledge doubling, however long it takes. It’s a shame his wisdom has a glass ceiling, forever a hindrance. What good is boundless knowledge, without the wisdom to use it? If a tree falls in the forest, which of us will be there with barrels full of superglue, to attempt to glue it back on its stump? You know, so the forest retains the appearance of a nice even growth pattern…otherwise it just wouldn’t be fair to the other trees.

  • Tom Cavanaugh

    The thought that your knowledge has doubled every 5 years has never crossed my mind.

  • Carl

    Today, “tech savvy” just means you are computer (or smartphone) literate. It doesn’t mean you have a sophistication about technology, or that you know “how things work”, especially from a mechanical, electrical, or fluid dynamic perspective. Engineers kind of need to know how everything works, and not just that “there’s an app for that.”

    A culture that has gotten fat and lazy, that feels entitled to a certain standard of living and of leisure time, without having to work or pay for it, is a culture destined to fail. The barbarian hordes are on their way…and they won’t warn us of our impending doom on facebook, so we will never see them coming.

    I saw a movie last night, “The Tourist” (silly, but then most are nowadays). I enjoyed seeing Paris, Venice…and Angie. But I couldn’t help but be reminded that France has invented high speed trains that are in regular use, and have been for a few decades…powered by an electric grid that is 80% nuclear. Contrast this with our Amtrak trains, who are run by a grid mostly powered by burning coal. They travel at a relative snail’s pace…all the while losing billions each year, subsidized by the taxpayer…adding to the debt. It also saddens me that I can’t even mail a letter or a package, without knowing I am adding to the national debt…all because the people in charge don’t know how to run things without losing money, nor do they care to learn. They can just print more greenbacks, because all that matters is the here and now.

    If that is a doubling of “knowledge” every 5 years, then I’ll be a monkey’s uncle…typing away, in a room full of my nephews and nieces on old typewriters, until we come up with a sequel to Hamlet, followed by the screenplay adaptation starring justin bieber, snookie, and tim tebow.

  • Carl

    I also stand by my assertion that a blind faith in mankind is misguided and will always lead to disappointment…and worse. That said, there’s nothing wrong with having a positive outlook, especially on real innovation. I personally am always enthusiastic to see a new gadget, especially if its meaningful. I am a camera geek, after all. I just don’t expect the future to always be better than the past. I try to stay informed about what business is doing, and especially what politicians are doing…along with what the rest of the world is doing.

    A university professor of engineering that I know, recently said that today’s undergrad students are a lot less sophisticated than the students of just a decade ago. He feels that all they know how to do, is walk around with their noses in their smartphones, texting, playing silly games…endlessly “socially networking”…or rather…gossiping and trying to get ***d. Can you imagine an undergrad in engineering, who thinks a screwdriver is only a drink, and has never seen the actual tool used to tighten and loosen screws? I’m not talking about students in non-technical fields, I’m talking about engineering!

  • Carl

    We are getting way off the topic of photography, and I will try to make these my last entry in this section.

    I don’t have a dim view of mankind in general, I just have a realistic view, so don’t be so sorry. I refuse to elevate humanity to some higher plane of consciousness than he actually has. I could even venture to say it’s possible the encyclopedia article from your anecdote, chose to provide vastly less space to an issue relating to Christianity (because of a change in attitudes from one generation of editors to the next)…rather than because mankind’s knowledge had somehow increased that many times fold, between editions.

    Even the idea of an encyclopedia has changed now, to one written by anonymous volunteer contributors, sometimes from the proverbial “parents’ basement”.

    Knowledge is lost and gained every day, especially historical knowledge. Occasionally it’s even hidden or re-written, usually to promote the political agenda of the historian. Sometimes those in high office do their part to promote such revisionism…and it can even help to spawn a political movement. (The one I have in mind is about 100 years old…)

    What you refer to as a “dim view”, is merely my reflection on historical reality. There was a reason for “the dark ages”. There’s no guarantee there won’t be more to come. I merely am stating my opinion, that you are too bold and optimistic in your assumption, that there will be an ever present continuation and progression of: culture, technology, knowledge, the free exchange of ideas…and especially of the free markets necessary for all of the above to exist and expand with minimum impediment (whether at an accelerating rate, or one nearer to a constant.)

  • Tom Cavanaugh

    From my own experience:

    When I was a kid, my parents bought a 1958 edition of the Encyclopedia Britannica. I once asked my mother how they figured out when Easter would be, so she took my hand, led me over to the Encyclopedia, we sat down and we found out together. The Britannica article describing how they did it was a little less that a quarter of the page, a little less that half of one column. In my highschool library, about 10 years later, I found a new edition of the Encyclopedia Britannica looked up the same subject, and the explanation was 4 lines long. There were the same number of volumes in the new edition than there were in the one I had as a child. Man’s knowledge had increased in the intervening 10 years that there were so many more things to write about, that they had to be more concise in the explanations.

    This “generalized cliche” has certanly been around for a while, and has often been repeated, but every attempt to quantify knowledge simply keeps validating it.

    I’m really sorry that you have such a dim view of mankind in general.

  • Carl

    You seem to be attempting to shift things around a bit, and put words in my keyboard which I didn’t type.

    You’re seeing the 8×10 print as a casual working piece, rather than something more formal, mounted in a frame. I kind of thought of 8×10’s as the original “portrait” size, at least since the era of the 4×5 film camera (since they are the same aspect). Perhaps people in the fashion and entertainment world use 8×10’s for work…I was just thinking of them where the “end user” sees them. Portraits of family members, framed…and NOT usually viewed at 12 inches.

    So I guess I wasn’t seeing someone hand-holding an 8×10 with their arm fully extended…because I wasn’t speaking about hand-holding them at all. I haven’t seen anyone holding one that way very often, since you asked…at least not since the last time I tried it in the mirror.

    Assuming such a generalized cliche is remotely accurate, do you honestly believe man’s “knowledge” will continue to “double” every 5 years, indefinitely? I don’t, nor do I put as much weight into such a platitude as you do. The increased ability to share knowledge, need not always guarantee a perpetual net increase, especially at an accelerating rate. Nothing on earth is forever, and in the end all knowledge is futile. Blind faith in mankind just might shorten your life, rather than lengthen it, or enrich it.

    Man has merely given birth to a new life form, which too often is just a novelty and a time waster. Its knowledge and processing power probably double every 1 or 2 years. That won’t continue indefinitely either. How do I know? Because physics are physics. That’s not how it happened in whatever sci fi story said otherwise? Well, I guess time will tell, won’t it?

    Man is really more interested in “social networking” and playing games, than he is at increasing his knowledge anyway. How often do you stream movies on your smartphone, and when you do, do you view it at the optimized distance to resolve every last pixel? If not, well then don’t even bother.

    We don’t know much more than we did in the 1930’s, regarding the basic design of an SLR. The basic idea hasn’t changed, it’s just been refined a lot. Hence the SLR design and layout, is a more MATURE technology than the small part that is a phase autofocus sensor. This was my point, and I feel like I’m beating a dead horse.

    Just because the film has been replaced by something newer, more convenient, and “better”, doesn’t mean the wheel has been re-invented. My other point was that phase autofocus is still in its relative infancy, when we see it in the conext of the time since the SLR, and even cameras in general, have been around. “Infancy” surely need not refer to the age of a human infant…since we don’t really call them infants much after age ONE…Technological development is almost always on a much longer time scale than human life (that seems obvious to me, so I wonder why it isn’t to you?)

    Some people don’t even see the SLR design as the end-all, be-all camera anyway. I happen to like it, though.

    As for your “25 year” figure…(given your own idea of 1985) you seem to be counting backwards from 2010, rather than 2000 like I was. I think of 2000, or early 2000’s, as the time when digital SLR cameras began their initial stages of displacing film cameras (which I’m pretty sure I hinted at…it was pretty obvious.)

    Don’t be too proud of this technological terror you’ve constructed…(to say more is to be sued by a trillionaire…)

  • Tom Cavanaugh

    How often have you seen someone looking at an 8×10 photo while holding it with their arm fully extended (about 2.5 feet)? It doesn’t happen. There arm is always bent at the elbow, greatly reducing the distance. While I don’t think much of the 12.8 inch figure either, I think it’s a lot closer than your “2 to 3 feet”, even if it is hanging on a wall.

    And as for your “Phase-autofocus sensors are also really still in their infancy”, 25 years is pretty old for an infant. (… and it’s even older if you believe Bell & Howell instead of Minolta.) Remember that Man’s knowledge doubles every 5 years. That means we currently know 32 times as much as we did in 1985, including how much we know about “Phase-autofocus sensors”. And on top of that, SLRs have been around since the 1930s. I leave it to you to figure out how much more we know now than we did then.

    How’s that for “Context”?

  • Carl

    Tom, thank you for the history of CoC, and for correcting me…sort of. My definition of “is” is different than yours. Really you have helped prove my statement you quoted, rather than refute it. I refer you to my original context (and stop quoting me out of it, ok?); I was speaking in terms of wide spread use and commercial viability. 15 years before 2000, could certainly still be defined as “slightly older”, when you compare the age of the SLR camera…and especially if you relate it in terms of other technology, such as audio (as I do too often!). Analog playback on disc is about 100 years old, so it’s a mature technology. Optical audio playback on disc, is barely middle aged by comparison, and yet is already being abandoned! The “camera” itself is nearing 200 years of age…It’s a mature technology, and yet has undergone transformation and renewal…so those new aspects of it are in their infancy of development…historically speaking. I mean, perhaps 15 years is a long time to a 20 year old…I just assumed I was speaking to readers with some life perspective…and stuff.

    The age of truly high performance autofocus (by my own standard anyway), is still in its “relative” infancy.

    And the first digital sensor dates back to the 1970’s, predating your Maxxum AF (in effect making us both wrong)…but were digital sensors in widespread use around 1985? No they weren’t…but you could have just as easily quoted me out of context on that too, if you wanted to…I thought someone would…but at least you didn’t do that!

  • Tom Cavanaugh

    Carl: “Phase-autofocus sensors are also really still in their infancy, only slightly older than digital sensors.”

    The Minolta Maxxum 7000, introduced in 1985, used Phase Detect AF.

  • Tom Cavanaugh

    Absolutely, but the CoC presumes a viewing distance equal to the diagonal measurement of the image. At smaller image sizes (4×6, 5×7, etc.) that’s not practical, but it’s presumed to be true for handheld images 8×10 and larger. I don’t think much of it myself, so it’s not me that’s doing the presuming, but that’s the way it is.

    See:
    http://en.wikipedia.org/wiki/Circle_of_confusion#Circle_of_confusion_diameter_limit_in_photography

  • Carl

    Tom, very interesting. In practice though, people will view an 8×10 from 2 to 3 feet, assuming it is framed and on a wall or otherwise on display, will they not? Not that they couldn’t lean in for a closer look. Of course, I guess people could lean in as close as their eyes can focus, if they wanted to, and had enough surrounding light to see the print. For me, this could be like 5 inches. So I’m not sure what “presumed” viewing angle means, but I guess there’s precedence for it.

  • Tom Cavanaugh

    Excellent article. You’ve made a lot of things more clear. But in doing so, you’ve made some pretty broad strokes, and I’d like to take issue with two of them.

    1. Pixel Pitch does not equal Pixel Size. There is unused space between the pixels, and sensor manufacturers have devoted significant effort to reduce this space by enlarging the pixels without changing the pixel pitch. Larger pixels with the same pixel pitch means better ISO performance and better Dynamic Range.

    2. Higher Resolution increases Depth of Field. Circle of Confusion calculations are an attempt to quantify perceptions after the fact. The formulas predate high resolution digital image sensors, so their predictions become less and less accurate as sensor resolutions continue to increase.

    You can test this for yourself. The 12MP Sony A700 APS-C dSLR with the Sony/Zeiss 85mm f/1.4 lens has about the same angle of view as the 24MP Sony A900 ‘Full Frame’ dSLR with the Sony/Zeiss 135mm f/1.8 lens. Both of these lenses are extraordinarily sharp. When stopped down to f/5.6, and focused at a subject 100 feet away, conventional DoF calculations would predict that the APS-C camera would have about twice the DoF of the ‘FF’ camera, but actual images will show very similar results.

    I’m not saying that the DoF formulas are wrong; I’m saying that our methods of determining the CoC don’t take into account hhigher resolution.

    Also, the presumed viewing distance for a 8 x 10 image is not 10 inches, but the diagonal size of the image, which is 12.8 inches.

  • David Rosenstein

    so, what is the best camera for IQ under $2000?

  • Carl

    So that leaves the reflex mirror camera as the main part of a “DSLR” that is more in its middle age. And yet this is the very part of a camera, which non-camera enthusiasts would like to get rid of, to save weight and size. They seem to outnumber serious photographers by an order of magnitude.

    Maybe another pertinent question should be, WHAT MAKES A SERIOUS PHOTOGRAPHER? (Apologies if there’s already been a similar article at LR…if so, there should be a new one!) Is it someone who demands that a “pro” camera be able to fit in a jacket pocket (or even exist only inside a smartphone)? I submit that answer is “no.”

  • Carl

    Pixel pitch, or size, does matter, probably more than most other aspects of a digital camera. The reason being light photons are always the same size…except that nobody really knows what size they are, or for that matter, WHAT they really are. So we describe them as packets of energy (matter?)…and sometimes (what is assumed to be a single photon) even appears to occupy two distinct locations at once!

    Signal processing matters too. Digital photography is still only in its infancy, it is not a mature technology. It really only took over the marketplace, from film, some time in the early or mid 2000’s, did it not? And I could be wrong, but I’m pretty sure current digital sensors (and processing) can’t outperform certain types of film in every area, most importantly the saturation and depth of colors higher than a certain “brightness”, however it is measured. (HDR doesn’t count here, that’s cheating!)

    Phase-autofocus sensors are also really still in their infancy, only slightly older than digital sensors. (I’m not speaking about the pre-historic digital sensors since the ’70’s, but only the ones that became commercially viable, again since 2000.)

  • Carl

    I found Roger’s blog post/article informative and not misleading at all, and actually agree with all of it. I basically had one further question and a few other observations, that apparently no one dares to substantively address :-D.

    Videography isn’t important to me, and I suspect that most of LR’s customers are “still” photographers (I could be wrong, but most of the lenses available here are not meant for video). And…to those people who refer to videography done with an APS-C or smaller camera, as “highend video”, that seems a bit delusional to me. “Highend video” is a question of perception, apparently. It also has more to do with the skill and experience of the loose nut behind the eyepiece…than with the hardware.

    To me it is amusing to read responses from those who had plenty of time on their hands over the weekend. They obviously feel a need to disagree and find fault…especially when they appear to assume some sort of sinister motive by the site owner…as if they are uncovering perhaps propaganda, or at the very least, intentional ignorance. It reminds me of my own point of view, back in the days I used to post on an audio forum, before I was banned…over a decade ago. Good thing I was getting bored with that…

    Roger has done an EXCELLENT JOB of stating the reasons why sensor size matters. The post was NOT about why “sensel” size matters, but that’s too often what such a discussion devolves into, since that is where the technological rubber meets the road.

  • Frank LLoyd

    For further reading, this is an excellent thread to follow:

    http://forums.dpreview.com/forums/read.asp?forum=1032&message=40625357

  • Roger Cicala

    Very pertinent points, Knickerhawk, those are rather dated studies. I was reaching back to my textbooks for some of that and should have tried to stay more up to date.

    The excellent comments by many of you have demonstrated, probably better than I did, that this is a complex subject and should be considered when making a new camera purchase. We’re reaching a time when we have a lot of choices to make in camera bodies, not just “there’s a new Canikosony body and I must have it”. What sensor and pixel size are just one consideration – but should be considered.

    The discussion has gone way beyond the intended audience – about 1/3 of the people who read this are primarily videographers who are have only recently realized that a 2/3″ sensor isn’t huge, and another 1/3 are, for the first time, considering a camera other than an APS-C sensor SLR. But I’ve enjoyed the comments immensely and have learned from them. As I’m sure others have too.

    Roger

  • Knickerhawk

    I overstated the extent to which you claimed bigger pixels are better. Sorry about that. Nevertheless, I think you would have served your readers better by providing some synthesis of the tradeoffs involved and Clark’s AIQ measurement is one example of that. By the way, the Chen article is from 2000 and I doubt that anyone in the field still believes the optimal pixel size is what that article predicted. Farrell only looked at noise performance for small sensels and only analyzed behavior at relatively slow shutter speeds. It didn’t purport to make claims about perceived IQ benefits of different pixel sizes and is also a rather old study.

←  Older Comments
 →
Follow on Feedly