Lenses and Optics
Just the Lenses: Canon and Nikon Mount 35mm f/1.4s
As I discussed in the last post, it’s impossible to accurately compare lenses from different mounts using any form of computerized target analysis testing (methods like DxO or Imatest). Target analysis tests an entire system (camera and lens). That’s a very practical thing, of course, but it has some limitations.
Directly comparing the lenses on an optical bench without any camera involved is interesting for several reasons. The most important is that the optical bench gives some information about a lens that is difficult or impossible to get using Target Analysis methods. Field curvature is a good example of information that is easy to get on an optical bench, but nearly impossible to obtain with Target Analysis. Plus, optical bench testing shows performance at infinity, rather than the closer focusing distances used for target analysis.
Direct lens comparison is occasionally of benefit for other reasons. Some people are thinking of changing brands – they know the other brand’s camera has higher resolution, but aren’t sure if the other brand’s lenses are as good (or vice-versa). More people than ever are shooting lenses across brands using adapters, and they’re curious about pure lens performance, too.
Optical bench comparisons are useful for those considering third-party lenses, too. People sometimes read a review of a third-party lens shot on Camera A and then are surprised it behaves differently on Camera B.
The 35mm f/1.4 prime lenses in Canon and Nikon mount make a good optical bench comparison. Canon and Nikon each have their own 35mm f/1.4, but photographers using either brand have several other excellent options including the Zeiss 35mm f/1.4, the Sigma 35mm f/1.4 Art, and the Samyang 35mm f/1.4 (AKA Rokinon and Bower).
Today’s Contestants
We tested seven copies each of the Canon 35mm f/1.4 L, Nikon 35mm f/1.4 G, Zeiss 35mm f/1.4, Sigma 35mm f/1.4 Art, and Rokinon 35mm f1.4 lenses on our Trioptics Imagemaster optical bench. All copies had been through our routine optical and Imatest screening and passed with flying colors.
From multiple past tests in our Imatest lab, we expected the Sigma 35mm f/1.4 would have the highest resolution, with the Zeiss and Canon versions just a little behind. We weren’t quite as sure what to expect from the Nikon and Rokinon 35mm lenses, although we expected them to also be quite good.
MTF Charts
It’s easy to look at Imatest or DxO numbers and say, “A has an MTF50 of 875 and B is 820, so A is better.” MTF charts give you a lot more information. That generally makes the summary a little more complex, which some people hate. But it also makes the summary a lot more useful.
If you don’t speak MTF, don’t worry. It’s not hard. Higher on the vertical axis is better. Dotted and solid lines of the same color close together are better (far apart is astigmatism). The horizontal axis goes from the center of the lens at “0” to the edge of the lens at “20”. Lower lp/mm have association with strong contrast, while higher lp/mm are associated with ability to resolve fine detail.

- Legend for all the MTF graphs
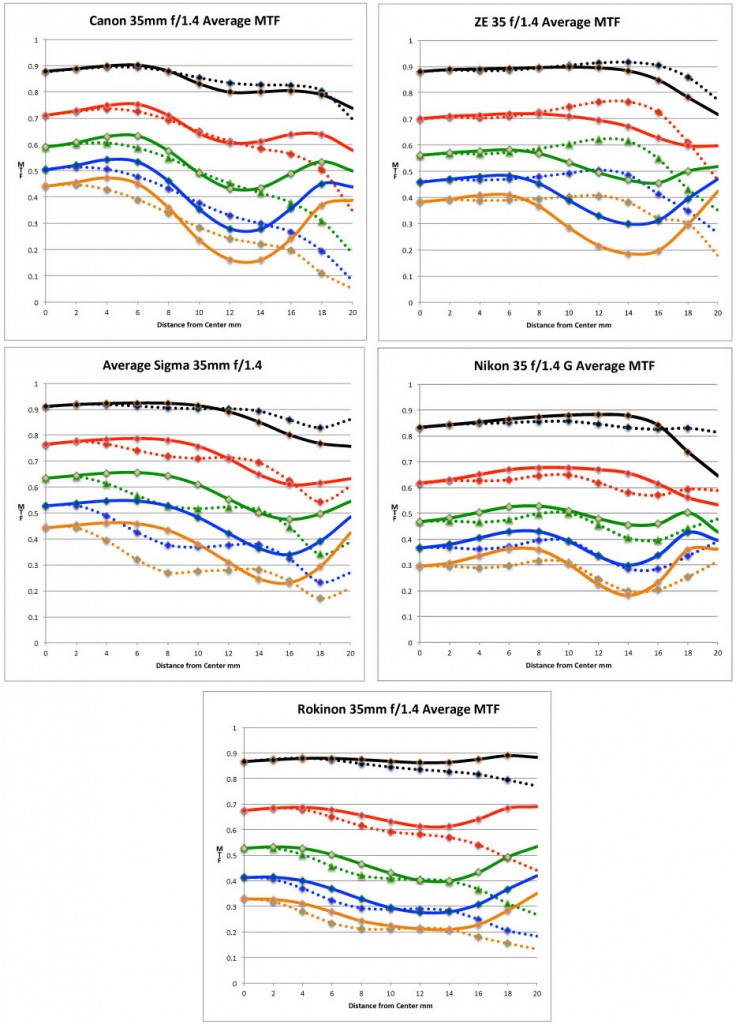
In general, the MTF graphs of the lenses on the optical bench agree with what we already assumed, although the differences are perhaps a bit greater than our standard MTF50 results suggested. The Sigma 35mm f/1.4 is clearly the sharpest lens of this group. Look carefully at the 20 lp/mm graph (red lines), for example. The Sigma stays above MTF 0.7 all the way to 12mm from the center of the image. The Canon and Zeiss lenses are competitive, although not quite as good away from the center. The Nikon and Rokinon lenses never get to 0.7 MTF on their 20 lp/mm graph, even in the very center.
While the Sigma does better than the Zeiss 35mm f/1.4 at higher frequencies (20-50 lp/mm) the differences between them aren’t massive. If you asked the inevitable “could you tell the difference in a picture” question, I’d answer “sometimes.” It would depend what you shot and how carefully you compared them.
The Canon 35mm f/1.4, despite being an older design, hangs pretty well with the Zeiss and Sigma. You can see there are differences, but certainly in the center 1/2 of the lens the differences aren’t huge. The Nikon and the Rokinon just aren’t quite as good as the other lenses, although they are still good lenses. (As we do some more prime tests, you’ll get to see some bad lenses where the differences are much more dramatic than these.)
If you go to DxOmark or another site that lets you compare the Canon 35mm f/1.4 to the Nikon 35mm f/1.4 G, you may find the Nikon rated slightly higher (depending upon which cameras were used for the test). That’s because the higher resolution camera gives the lens-camera combination a much higher rating.
You can also compare the Rokinon or Zeiss lenses on different camera bodies. Although the lenses are identical, again the camera-sensor combination will give a higher resolution value to the lens shot on the higher resolution camera. (As an aside, we tested both Nikon and Canon mounts for the Zeiss and Rokinon lenses in this test. They were identical on the optical bench, as they should be.)
Let me point out one other thing I think you’ll find interesting. Notice, especially in the Canon MTF graph, how it “dips” in the area from 10 to 16mm off axis, and then sharpens again in the corners? To a slightly lesser extent the other lenses do something similar (in the Zeiss lens it becomes an area of increased astigmatism). You want to know why that happens, don’t you? OK, I’ll show you why.
Field Curvature
We also ran field curvature tests on all the lenses. If you haven’t seen these graphs before, they’re a bit different than the MTF curves. (You can read more about them here.) Most people think of field curvature in kind of general terms, but tend to forget that the tangential and sagittal fields can have very different curvature and that the curves can be complex or simple. A perfectly flat field is actually rather rare.
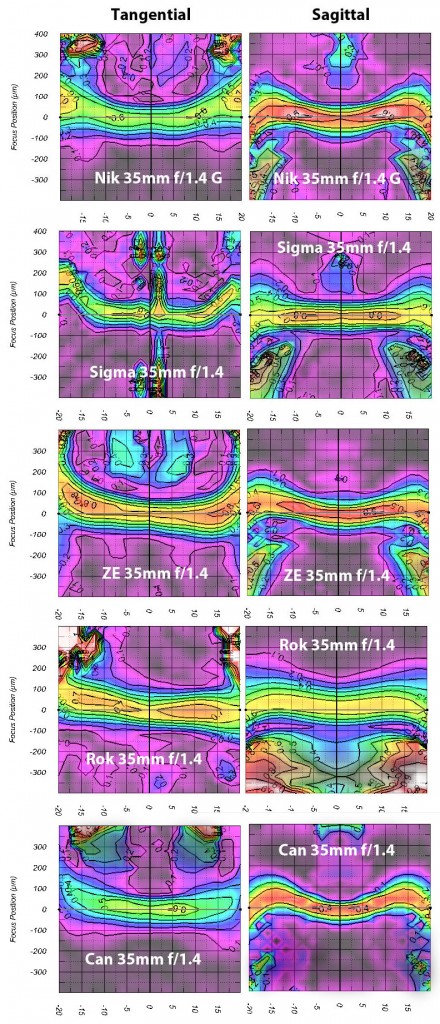
There wasn’t a lot of shocking information in the field curvatures. The Canon has a complex ‘moustache’ sagittal curve. If you notice, the area of the moustache is the same area where the MTF curve “dips.” Since MTF of the entire lens is measured at best center-point focus, the field (or plane of focus, if you’d rather) curvature makes the MTF numbers dip in this region.
I know some of you are immediately going to say that the MTF is higher if we focused on that point, instead of using the center point. That is correct; when we recheck focusing specifically on that area the MTF numbers are higher. In practice, though, you’d have to have a “moustache” shape subject of interest, though, to get it all in best focus at the same time. On the other hand, if you were using the camera’s AF point at that location, your image would look better in that area than the MTF curve suggests it would (at the expense of making the center of the image out-of-focus).
The Rokinon lens, while it has a lower MTF than most of the other lenses, has a very flat field. The Zeiss field is fairly flat, too, except on the very edges. The Sigma has a very flat sagittal field, while the tangential field curves at the edges of the image. The Nikon is fairly flat until the edges, but there the sagittal and tangential fields curve in opposite directions.
Why does this matter? If I were shooting a flat architectural feature I might find the flatter field lenses to be superior to the others, even though their MTF is not quite as good. If I had an area of interest out in the outer 1/3 of my image, and another in the center (a row people for a group portrait, for example), it’s going to be difficult to get both in focus with the Canon. See, this Geeky stuff does have some practical uses.
Oh, I also know 614 people are going to mention that you can just stop down the aperture and overcome that field curvature. Before you write that snarky note, are you absolutely certain that stopping down doesn’t change the field curvature? What if stopping down accentuates that moustache distortion? Are you sure that doesn’t happen? That sounds like the subject of some future blog posts, doesn’t it? So all 614 of you, hold that snarky comment. You might be glad you did.
Corner-to-Corner Variance
One nice thing that the optical bench does is give us very precise measurements at each of the 4 rotations that we measure for each copy of the lens. By comparing the 4 different measurements taken on each copy, we can get a very accurate measurement of the difference between the sharpest and softest side or corner.
- Testing each copy at 4 rotation angles gives us an excellent way to tell how even each side and corner is.
For each lens, we calculate the difference between its highest and lowest MTF at each position — basically a very accurate way of determining how different the worst corner is from the best corner. We then average this difference for all of the copies of each lens tested. (Every lens, when measured to this degree of accuracy, is slightly different in the worst and best corners, although you’d have trouble telling it on a photograph.)
Before I show them to you, raise your right hand, look into the monitor and repeat after me: “I do solemnly swear not to make the stupid mistake of assuming the following information applies to lenses other than the 35mm f/1.4 lenses being discussed. I especially swear not to make a statement that one brand is better than another based on this one lens’ data, because I realize that Roger has already tested a lot of other prime lenses that he hasn’t written up yet.”
The following graphs should be simple to follow. The horizontal axis is change in MTF, so if you see a point on the variance graph that has a value of 0.1, that means the MTF at that position varies by 0.1 on the average copy of that lens. The MTF reading we show in the graphs above is for the average of all 4 rotations positions. So if the MTF graph says the MTF at that position is 0.7, and the variance is 0.05, then a single copy of the lens would have an MTF of 0.75 at its best corner, and 0.65 at its worst corner (or side, or whatever position it is).
Every single copy of every lens we’ve ever tested has a best and worst corner (or side, or whatever). None have ever been absolutely equal. They are just equal enough that you don’t notice it in a photograph. But lenses with lower variance (remember, the variance is the average variance of many copies) tend to have more similar corners, while lenses with high variance have more differences.
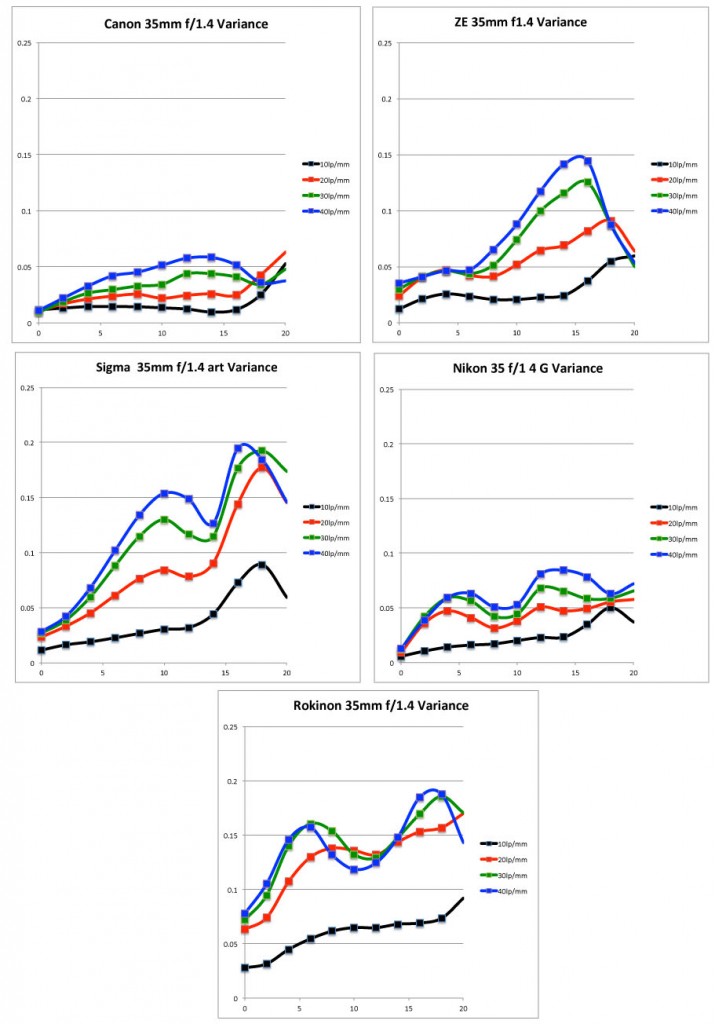
A quick glance at the charts shows you the Canon and Nikon 35mm f/1.4 lenses have less variance than the others do. I know some of you are just dying to say that’s because your favorite manufacturer has better quality control. Trust me on this, as I write up more of these prime lens results you’ll see that generalization isn’t accurate. When we do other focal length prime comparisons you’ll see the “low variance” supplier changes depending on which lens we’re considering.
Some of you are screaming that there’s something wrong with the Zeiss results because you absolutely know that Zeiss lenses have the best quality control. (They probably do, actually, but there’s more going on here than just QC.) The Sigma and Rokinon have a bit more variance, probably enough that on the average copy you could detect one slightly softer corner if you did some pixel-peeping tests.
Remember that optical designs that give very high resolution sometimes require tighter tolerances. In some cases, a design with slightly lower resolution has wider tolerances. Put another way, a 0.01 degree tilt in a given element may have a much larger effect in the highest resolution lens and a smaller effect in a lower resolution lens.
Remember also that the amount of optical adjustability built into a lens differs. Some lenses have six different elements than can be adjusted to fine-tune copy-to-copy variance. Others have none; what you get is what you get. That can be a two-edged sword, of course. Having too many optical adjustments may make things so complex that it’s hard to get them all done just right.
Until I publish some more of these prime results to give you enough comparisons to draw your own conclusions, let me say all five of these lenses are pretty reasonable. The Canon and Nikon 35mm f/1.4 lenses are two of the lowest variance prime lenses we’ve tested (we’ve done about 30 so far). The Sigma and Zeiss 35mm f/1.4 are about average, while the Rokinon is slightly worse than average.
Summary
The optical bench results for the Sigma 35mm f/1.4 lens show that it does has the best MTF, as most testing suggests. All of these lenses are quite good, however, and the Canon and Zeiss lenses aren’t far behind the Sigma.
The field curvature may be a bit surprising to many of you, and may actually be of more practical value than the MTF results. We’ll be discussing the field curvature of these lenses a bit more in the next post.
The variation between best and worst areas on each lens is amazingly good for the Canon and Nikon lenses. The Sigma and Rokinon 35mm f/1.4s have a bit more variation, enough so that on most copies, if you really, really tested carefully, you could probably detect one corner a bit softer than the other. I doubt you’d see it in a photograph for the “average” lens, but since the variance is higher, there’s probably a higher chance of getting a copy with a corner soft enough to notice in photographs.
Over all, though, all five of these lenses are very good from an MTF standpoint. Some are better than others, obviously, but price range, bokeh, and a number of other factors will make a bigger difference than the MTF for a lot of photographers.
Roger Cicala and Aaron Closz
Lensrentals.com
September, 2014
Author: Roger Cicala
I’m Roger and I am the founder of Lensrentals.com. Hailed as one of the optic nerds here, I enjoy shooting collimated light through 30X microscope objectives in my spare time. When I do take real pictures I like using something different: a Medium format, or Pentax K1, or a Sony RX1R.
