Geek Articles
Painting Zoom Lenses with a Broad Brush – Roger’s Law of Wide Zoom Relativity

I’ve been writing peer-reviewed scientific papers for way longer than I’ve been blogging about optics. I value significant numerical information presented with methods that allow reproducibility as much as anybody. But way too many people who can’t define either spurious accuracy or spurious resolution believe (and unfortunately create) nonsense numbers on the internet and repeat them as though they mean something.
So I decided to write a post that presents some data from over a hundred lenses, but without any specific numbers, and nothing that says a given lens is better or worse than anything else. (And yes, I’m fully aware that tomorrow someone will link to this post to claiming I said one of these lenses is way better than another. As best I can determine I’ve only said about 30% of what I’m said to have said).
So why would you bother reading it? Because I bet by the end of it, I will show you something you probably didn’t know about zoom lenses. While it’s geeky, it might actually be useful to you. So this is a post for everyone. If you hate numbers, there aren’t any. If you want to learn a general law of lenses, I’ll show you one. If you like looking at beautiful landscape images and discussing photographic technique, well, OK, then it’s a post for almost everyone.
So What are We Going to Do Today?
Well, let’s take a pricey optical bench, add nine copies each of a bunch of zoom lenses. Let’s measure the MTF, not just across the middle but also from top-to-bottom and corner-to-corner. Rather than give you the several hundred MTF numbers that generates for each lens, I’ll just plot one frequency in a graph. (The frequency is 30 line pairs/mm, which is a good frequency because it’s relatively high resolution, suitable for today’s high-resolution sensors). And I’ll just map the sagittal numbers because it cuts the number of graphs in half and the conclusions are the same either way. So one lens, tested at one focal length would look like this.
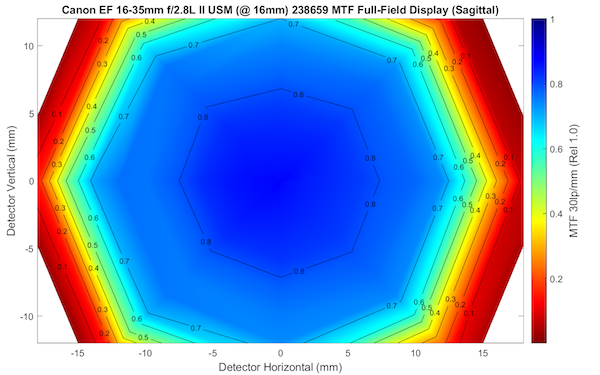
Olaf Optical Testing, 2017
In the center, where things are blue, the MTF is pretty high, 0.8 or greater. At the edges, where things are red, the MTF is very low, 0.2 or less. This is actually a very good copy of this lens at 16mm, quite sharp in the center with the inevitable blurring in the corners that is the hallmark of it’s kind. But, as I’ve often said, zoom lenses vary. So let’s look at thumbnails of 9 more copies of the same lens, the Canon 16-35 f/2.8 Mk II at 16mm. Why thumbnails? Because we don’t need to look at details here; we’re just getting an overview.
Olaf Optical Testing, 2017
All of those lenses easily passed our screening tests and are good copies. On the highest resolution test charts on a 5Ds, even the top center one passes. But you can see each is a little bit different than the others.
Now let’s take those ten lenses above and average them together, so we get a picture of what a ‘typical’ Canon 16-35mm f/2.8 Mark II should look like. As you may have noticed, just to amuse myself, I chose the ‘most typical’ copy for the image above; it looks almost identical to the average one below.
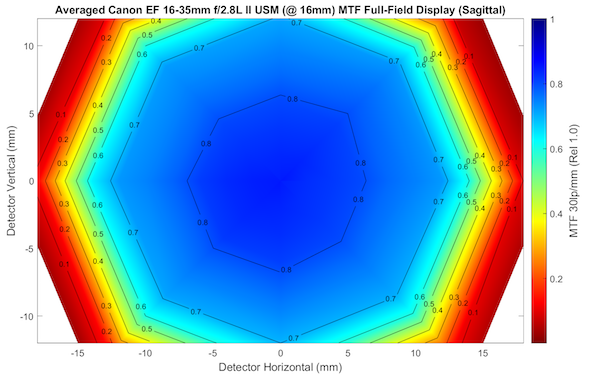
Olaf Optical Testing, 2017
From here on out, when I show you a graph of a lens, it will be an average of 9 acceptable copies of that lens. The definition of ‘acceptable’ changes depending upon the lens and the focal length, of course, because not all lenses are equal, and a given lens isn’t equal at different focal lengths. But that’s what we’re here to talk about.
There is one thing I want to repeat. This is partial data; we’re looking at one MTF frequency and only the sagittal MTF at that. Don’t go fanboy and try to use this to do a lens comparison. It’s representative of the other frequencies, and tangential data follows a roughly similar path. But using these pictures to say this lens is better than that lens is, well, fanboy drivel.
So What Happens at Other Focal Lengths?
Well, we started with the Canon 16-35 f/2.8 Mk II at 16mm, so let’s look at it at 24mm, and 35mm, too. This should surprise none of you, we’ve known for a long time this lens was sharpest at 16mm and then softens up as you zoom in. It’s actually a tiny bit better at 35mm than it is at 24mm, but neither focal length is nearly as sharp as 16mm except at the very edges.
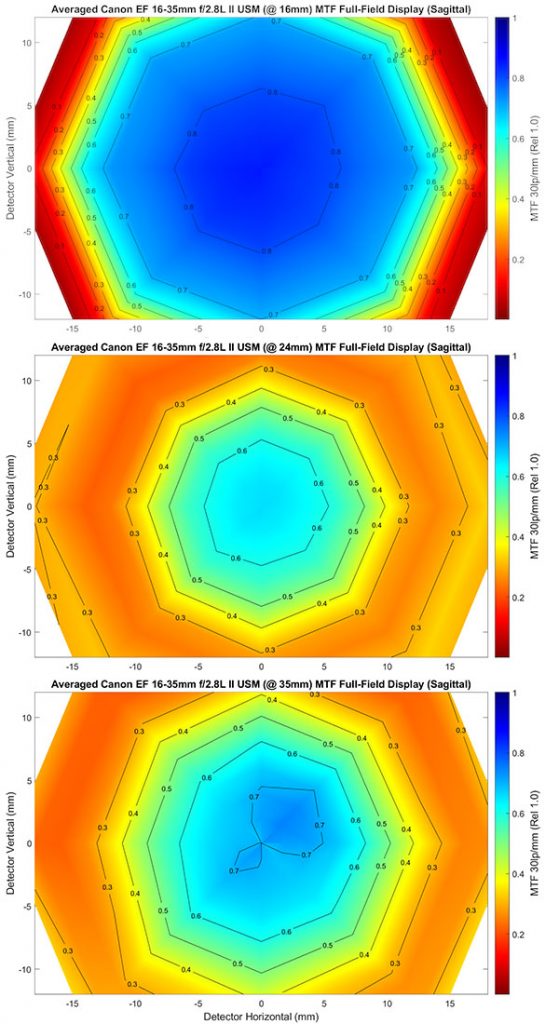
Olaf Optical Testing, 2017
Now the question you should be asking, or at least the question I would be asking, is “Did they all get softer or did some get really soft and bring the average down”? I’ll just tell you that at 24mm they basically all got softer, but at 35mm there was a combination of softening and more variation. Here are the thumbnails of the lenses that went into making up that average.
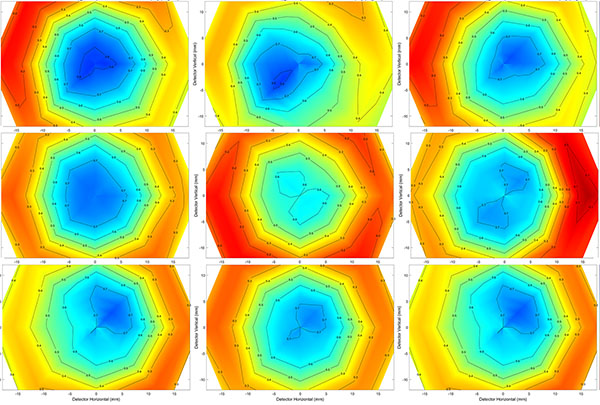
Olaf Optical Testing, 2017
So there is more variation at the long end, but none of these 9 are as good at 35mm as they are at 16mm. The takeaway point is the Canon 16-35mm f/2.8 Mk II is best at 16mm and then gets weaker at longer focal lengths.
So let’s compare that to some of the other wide-angle zoom options. (Oh, and because someone will ask, I’m using an average of 9 because that’s plenty to show the tendency here. I’ve done it with lots more copies, and the averages don’t change much.)
What About Other Wide-Angle Zooms?
I know you all want your zooms to be even at all focal lengths, so let’s look at your shopping choices among the wide angle zooms and see if we can find that. Below I’ve placed the average graphs at 16mm, 24mm, and 35mm for the Canon 16-35mm f/2.8 III and the 16-35mm f/4 IS Canon lenses. Remember, the f/2.8 lens is tested at f/2.8; it would be somewhat sharper if tested at f/4.
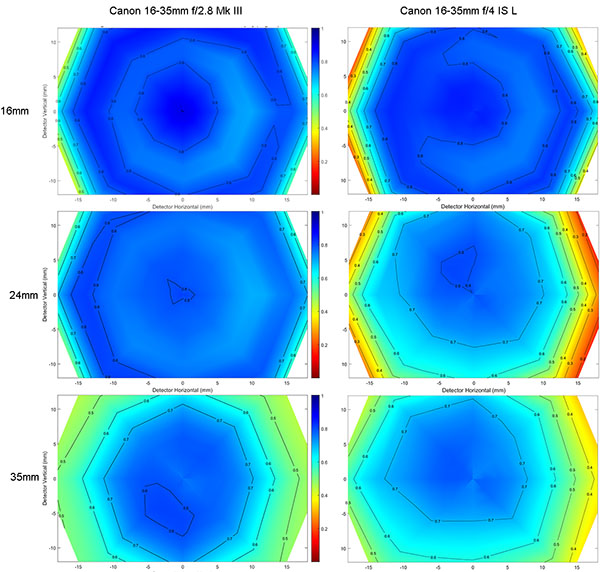
Olaf Optical Testing, 2017
Both of these retain more sharpness at the longer focal lengths than the older design does. In fact, the 16-35mm f/2.8 Mk III is indistinguishable at 16mm and 24mm, losing a bit of sharpness at 35mm. The quick takeaway message is the new lenses are probably worth the upgrade from the Mark II; they don’t fall off as much as you zoom in. But I’ve got more of a point to make, so let’s continue
Let’s take a look at two third-party options in roughly this focal length; the Tokina 16-28mm f/2.8 AT-X Pro and the Tamron 15-30mm f/2.8. I’m doing these just at the two extremes of focal length here.
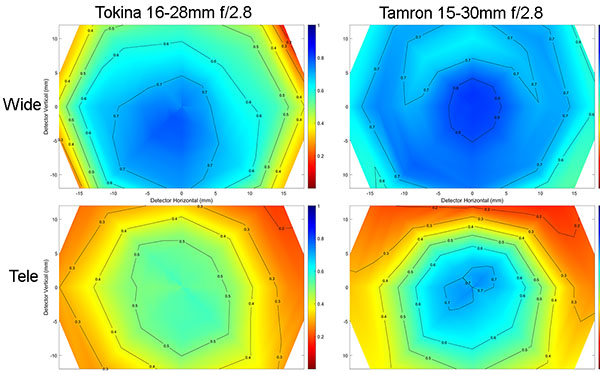
Olaf Optical Testing, 2017
You may be starting to see a pattern here; sharper at the wide end, weaker at the long end. How about some Nikon wide zooms. Nikon tends to design somewhat differently; maybe they don’t have this pattern.
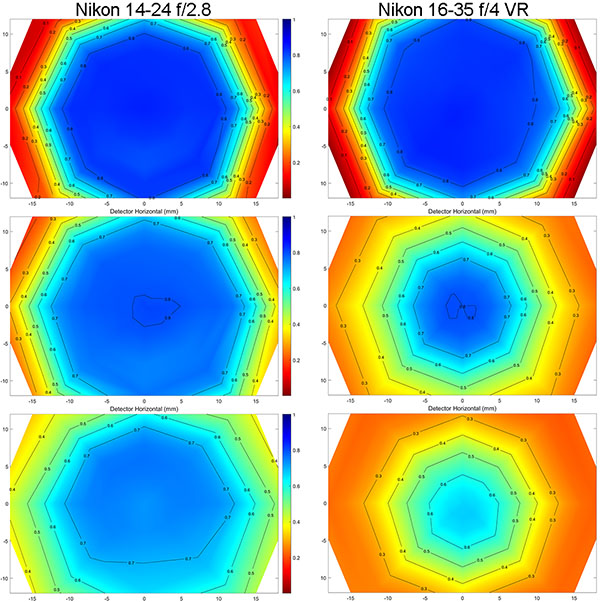
Olaf Optical Testing, 2017
Well, the Nikon’s show the same typical pattern, sharpest at the wide end, softer at the longer end. Like the Canon 16-35mm f/2.8 Mk II, the Nikon 14-24 f/2.8 is better at the edges at 24mm, but the central half of the image is softer. The edge improvement may be an effect of less field curvature than anything else, but I won’t argue the point.
I have data on two more wide zooms I’ll throw up in the same graph. They have nothing in common, they’re just the two I haven’t shown yet, and two lenses fit reasonably well into one image. The Canon 17-40mm f/4 L is an old design; the Sigma 12-24 f/4 Art is a very new one. (BTW we now test 2X or fewer zooms only at the two ends, which is why there’s no middle data for the Sigma).
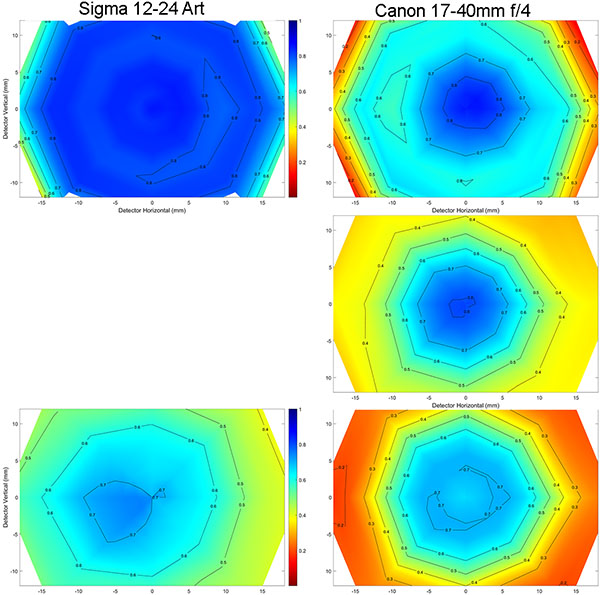
Olaf Optical Testing, 2017
At this point, I think, the pattern is pretty clear. For simplicity sake, I think it best we give this pattern a name, and I think the logical name would be “Roger’s Law of Wide Zoom Relativity” since wide zooms are relatively sharper at the wide end. Are there exceptions to this law? Yes, but they are few and far between. For a few of these sets of 9 copies, there’s one lens that’s better at the long end than at the wide end, but for most there are none. No set tested averaged better at the long end than at the wide end.
Is this useful to know? Yes, it is. If you’re going to test your brand new lens, either by taking pictures or using a test chart, test the long end. If the lens is weak, that’s where it will be weakest. With some of these lenses where the difference is great, you might consider shooting at the wider end you can, either by foot-zooming a little closer or by changing to another lens when appropriate.
I know what you’re thinking now, though. You’re thinking, well, that’s just for wide zooms, right? Let’s take a look.
Standard Range Zooms
I’m not going to bore you with lots of text; you’ve got the drill now. I’m just going to show you graphs. Like the ones above, the wide end is on top, the longer end on the bottom.
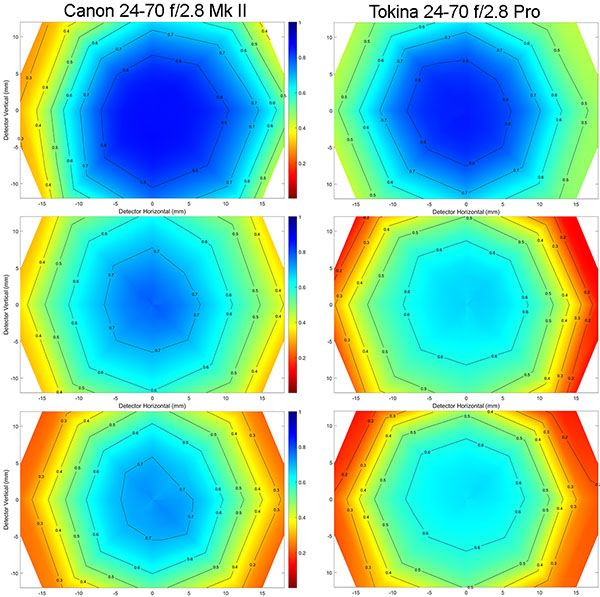
Olaf Optical Testing, 2017
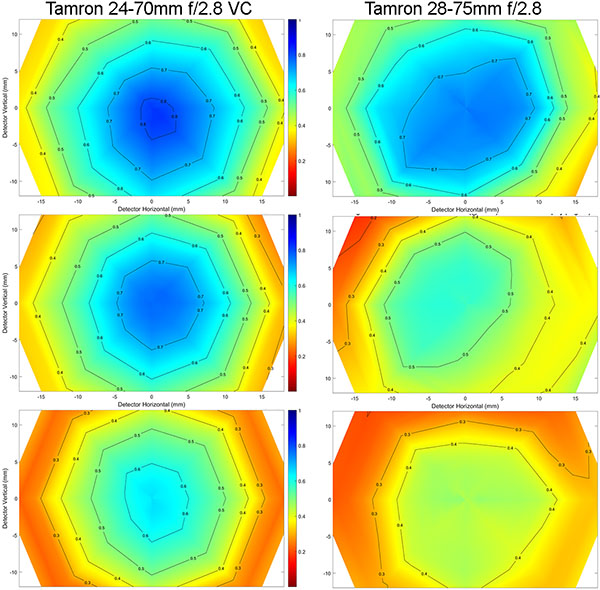
Olaf Optical Testing, 2016
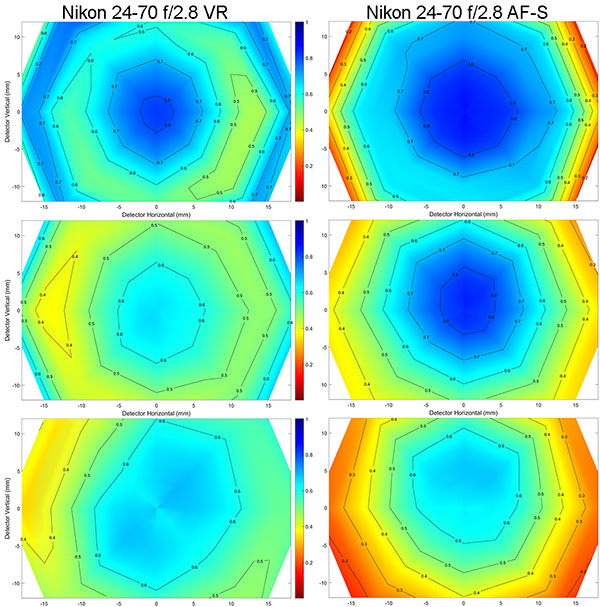
Olaf Optical Testing, 2017
The graphs for Sony lenses can look a little different because at some focal lengths the built-in baffles cut off some of the edges, but the same thing happens – better performance at the wide end.
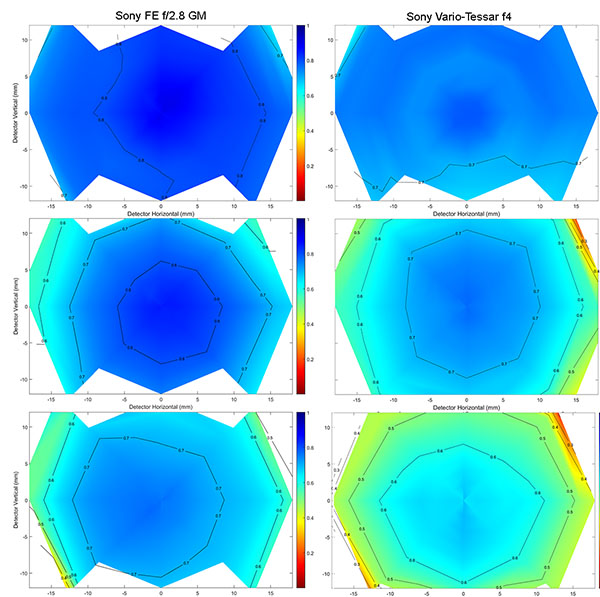
Olaf Optical Testing, 2017
Again, you can see the pattern; standard range zooms tend to resolve better at the wider end, not as well at the telephoto end. I didn’t show them, but 24-105mm and 24-120mm zooms have the same pattern. So the Law of Wide Zoom Relativity seems to hold true for zooms that go from wide to slightly telephoto. I can’t tell you if it’s true for superzooms, like 18-270s, because I will never, ever test them. Life is too short to test 10x zooms. I can tell you that it’s not true for 70-200 zooms, but that’s the subject of a future post.
So what does this mean for actual photography? For me, it means I shoot my wide zoom at the wide end as much as possible and reach into my bag for the 24-70 zoom when that’s an option. The choice is a little less clear when things approach 70mm, and the choice becomes a 70-200mm lens, but, as I said, we’ll consider that later.
Why Might This Be So?
This seems a bit counter-intuitive, doesn’t it? Historically, it’s been harder to design wide-angle lenses, and with prime lenses, we tend to accept that wide-angles will be less sharp, at least in the corners, than longer lenses. So I would have expected the wide end to be less sharp in these zooms, or maybe that some would be better at one end than the other. But what we saw was 17 zooms tested, 17 sharper at the wide end. (You might argue about 2 of the 17 having better edges at the long end, but not better overall resolution.)
I can’t say for certain why this would be so, but you know me, I’m happy to speculate.
All zooms, whether they have an extending barrel or not, have at least two elements (and usually more) that move during zooming. The elements move along helical tracks, rotating as they go. Moving elements away from each other can magnify aberrations, which would reduce MTF, of course. The lens designer would attempt to correct for that, but lens design is always a compromise. The simple act of moving an element might tilt it or alter spacing from ideal.
However, there’s no reason I know of to think one position is better than the other. The movements of the zoom elements are usually complex. It’s not as simple as ‘when you zoom in, elements move further away from each other.’ If only the extending barrel zooms acted this way, then that might have something to do with it, but that’s not the case. A couple of these actually extend to get to the wide end and are ‘at rest’ in the center of the zoom range.
Lens design probably has more to do with it. Zoom lenses are designed, as best I understand, from a starting focal length. Then the design is modified to allow it to zoom, then corrections made for the aberrations that the zooming created and the cycle repeats until either the lens designer’s deadline hits or the marketing department is satisfied. It would make sense to start the design at the widest end which is probably the more difficult to design. That might, then, remain the better end when the design is complete.
The complexity of designing the wide end is probably less today with modern lens-design software, but in the optical industry, old habits die hard. If the practice was to begin a design at the wide end, that’s probably still the practice now. Not to mention the reality of lens design is that the designer usually begins with an existing lens, then modifies it. They rarely start the design from scratch.
Finally, and I know more about this than I do about lens design, there is the optical adjustment of the lens. For every zoom lens the adjustments are done at the wide end first, then a set of separate and more limited adjustments are done at the long end. But the rule of ‘get the wide end right, then tweak the long end’ is pretty universal for zooms.
So, to summarize: I don’t know why, exactly. The above was just me speculating on some logical reasons.
But I think it’s a useful and interesting thing to know, and something I’ve never heard talked about. With very, very few exceptions, every wide and standard range zoom is sharpest at it’s widest end.
Roger Cicala, Markus Rothacker, Aaron Closz, and Brandon Dube
Lensrentals.com
March, 2017
Addendum: Just because I know it’s coming, let me take a moment to comment on the inevitable people who will say, “I know you presented thousands of data points on hundreds of lenses, but you’re wrong because I have one that’s different.”
You actually might. Depending on the lens type tested between 0% and 15% are actually sharper at the long end. It does happen. It’s just not the general rule.
Second, we consider the fact that we see more detail when we zoom the lens to be the same as sharpness. If my subject fills up 10% of the frame and I zoom in, so it fills up 30% of the frame, I will see more detail. That’s not the same as sharpness. What the data I showed says is, within reason, if you shot an image at 70mm, then moved so that you had exactly the same framed image at 24mm, the 24mm image would have more detail.
And third, especially with wide zooms, if you shoot a test chart make sure you shoot different sizes of the same chart at the same distance. If you get close to a chart at the wide end, you may start approaching minimum focusing distance where lenses are less sharp.
Author: Roger Cicala
I’m Roger and I am the founder of Lensrentals.com. Hailed as one of the optic nerds here, I enjoy shooting collimated light through 30X microscope objectives in my spare time. When I do take real pictures I like using something different: a Medium format, or Pentax K1, or a Sony RX1R.
-
Roger Cicala
-
Roger Cicala
-
Roger Cicala
-
Roger Cicala
-
Brian Caldwell
-
Itai Basel
-
Itai Basel
-
Don Farra
-
Geoffrey Forrest
-
Geoffrey Forrest
-
Geoffrey Forrest
-
Geoffrey Forrest
-
Geoffrey Forrest
-
Geoffrey Forrest
-
Geoffrey Forrest
-
Kevin Sparks
-
Dragon
-
GF
-
Ralph Wallace
-
Rob. S.
-
pmpm12345
-
Magnar W. Fjørtoft
-
Perry Winkle
-
Roger Cicala
-
?ukasz Moszczy?ski
-
Roger Cicala
-
Marcello Mura
-
Marcello Mura
-
tresemes
-
Athanasius Kirchner
